I.3. Soluţie:
Cazul I: Dacă vectorul 
este coliniar cu
vectorul 
(
) atunci există 
astfel încât:
|
|
(I.3.2) |
Înmulţind scalar cu vectorul ambii membri ai
relaţiei (I.3.2) se obţine:
|
|
(I.3.3) |
Din relaţiile (I.3.2) şi (I.3.3) rezultă că
vectorul poate
fi scris sub forma:
|
|
(I.3.4) |
deci relaţia (I.3.1) este verificată.
Cazul II: Dacă vectorii şi nu sunt coliniari (
), atunci vectorul poate fi descompus în
două componente: componenta 
coliniară cu vectorul (
) şi componenta 
ortogonală pe 
(
):
|
|
(I.3.5) |
Notăm cu: 
versorul vectorului şi cu 
unghiul format de vectorii şi 
. Dacă 
(figura I.32) atunci se obţine:
|
|
(I.3.6) |
 |
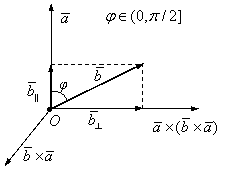Figura I.32.
 |
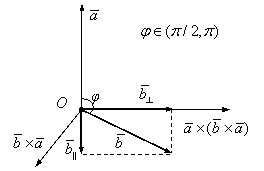Figura I.33.
În cazul în care 
(figura I.33) avem:
|
|
|
|
|
(I.3.7) |
Din (I.3.6) şi (I.3.7) rezultă:
|
|
(I.3.8) |
, 
Înmulţind vectorial ambii membri ai relaţiei
(I.3.5) cu vectorul ,
întâi la stânga şi apoi la dreapta, se obţine:
|
|
(I.3.9) |
Din relaţia (I.3.9) rezultă că vectorii 
şi sunt coliniari şi au acelaşi
sens. Vectorul poate
fi scris sub forma:
|
|
(I.3.10) |
Deoarece 
şi 
, rezultă că 
şi 
. Înlocuind aceste relaţii în (I.3.9), se
obţine modulul vectorului sub forma:
|
|
|
|
|
(I.3.11) |
Din relaţiile (I.3.11) şi (I.3.10) se obţine
vectorul proiecţie ortogonală pe a vectorului sub forma:
|
|
(I.3.12) |
Din (I.3.5), (I.3.8) şi (I.3.12) rezultă că un
vector oarecare ,
necoliniar cu ,
poate fi scris sub forma (I.3.1):
|
|
(I.3.13) |
Deoarece relaţia (I.3.1) este verificată şi în
cazul în care vectorii şi sunt coliniari, rezultă că această relaţie
este satisfăcută pentru orice vector 
.
Observaţii:
1º. Din relaţia (I.3.1) se obţine:
|
|
(I.3.14) |
Se observă că această relaţie este satisfăcută
şi în cazul în care 
.
Deci:
|
|
(I.3.15) |
ţinând cont de: 
, relaţia (I.3.15)
este echivalentă cu:
|
|
(I.3.16) |
2º. Relaţia (I.3.16) se extinde pe mulţimea vectorilor liberi:
|
|
(I.3.17) |
 |
  |