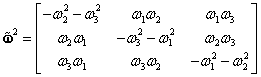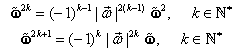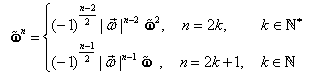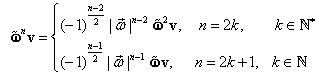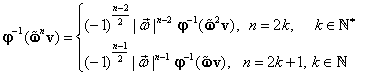III.4. Soluţie:

            În spaţiul liniar  considerăm o bază ortonormată dreaptă . În această bază vectorii  admit descompunerile:

	(III.4.2)
	(III.4.3)

            Notăm cu  matricea antisimetrică asociată vectorului  (III.2.81):

,

(III.4.4)

şi cu  matricea coloană a componentelor acestui vector (III.1.4):

,

(III.4.5)

            Deoarece baza  este ortonormată, au loc relaţiile (III.2.83) şi (III.2.84):

	(III.4.6)
	(III.4.7)

            Prin inducţie matematică după  se demonstrează:

(III.4.8)

            Deoarece aplicaţia  este bijectivă, din (III.4.8) rezultă:

,

(III.4.9)

 

            Pentru a demonstra relaţia (III.4.1) se determină în continuare expresia matricei , .

            Pentru o matrice pătratică de ordinul 3, , , polinomul  se numeşte polinom caracteristic şi are forma:

,	(III.4.10)

            Coeficienţii  reprezintă invarianţii principali ai matricei A şi au expresiile [**bib**]:

	(III.4.11)
	(III.4.12)
	(III.4.13)

unde  reprezintă urma matricei A şi este egală cu suma elementelor de pe diagonala principală a matricei.

            Ecuaţia:

(III.4.14)

se numeşte ecuaţia caracteristică a matricei A.

            Rădăcinile acestei ecuaţii se numesc valori proprii ale matricei A. Pentru o matrice pătratică de ordinul 3 cu elemente numere reale ecuaţia caracteristică este ecuaţie algebrică cu coeficienţi reali de are gradul 3. O matrice  are 3 valori proprii reale () nu neapărat distincte, sau o valoare proprie reală () şi celelalte două valori proprii numere complexe conjugate (, ).

            Teorema Cayley-Hamilton [**bib**] precizează că orice matrice pătratică cu elemente numere reale satisface ecuaţia sa caracteristică.

            Pentru o matrice pătratică de ordinul 3, , se obţine:

(III.4.15)

 

            Ecuaţia (III.4.15) permite exprimarea matricei  ca o combinaţie liniară a matricelor ,  şi . Prin inducţie matematică după  se demonstrează că pentru orice  matricea  poate fi scrisă ca o combinaţie liniară a matricelor ,  şi . Dacă matricea A este inversabilă atunci proprietatea se extinde pentru .

 

            Aplicăm procedeul prezentat mai sus pentru a determina matricea , , pentru matricea dată prin (III.4.4).

            Prin calcul direct se obţine:

(III.4.16)

de unde rezultă:

(III.4.17)

            Deoarece baza considerată în spaţiul liniar al vectorilor liberi este ortonormată, din (I.22.21) se obţine:

(III.4.18)

astfel încât relaţia (III.4.17) devine:

(III.4.19)

            Aplicând relaţiile (III.4.11)-(III.4.13) se obţin invarianţii principali ai matricei :

	(III.4.20)
	(III.4.21)
	(III.4.22)

            Ecuaţia caracteristică a matricei  este:

(III.4.23)

            Aplicând teorema Cayley-Hamilton:

(III.4.24)

rezultă:

(III.4.25)

            Prin inducţie matematică după  se demonstrează că puterile matricei  sunt date de:

(III.4.26)

            Se obţine în continuare:

(III.4.27)

            Utilizând expresia (III.4.27) rezultă:

(III.4.28)

            Pe baza liniarităţii aplicaţiei  se obţine:

(III.4.29)

            Relaţiile (III.2.85) şi (III.2.86) arată că:

	(III.4.30)
	(III.4.31)

            ţinând cont de (III.4.29)-(III.4.31), relaţia (III.4.9) devine:

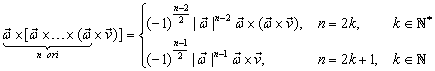
(III.4.32)

deci relaţia (III.4.1) este verificată.

---

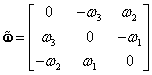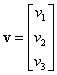GO TOP