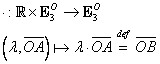Capitolul I

Calcul vectorial

A. Breviar teoretic

Modelul matematic al spaţiului absolut al mecanicii clasice este spaţiul euclidian, punctual, tridimensional, notat . Folosind noţiuni primare (punct, dreaptă, plan, etc.) şi un set de axiome se construieşte teoria axiomatică a geometriei euclidiene. Vom presupune cunoscută această geometrie la nivelul predat î în liceu. Considerăm ca fiind o mulţime ale cărei elemente sunt puncte.

1. Mulţimea segmentelor orientate

Definiţia 1:

Se numeşte segment orientat un element al produsului cartezian .

Un segment orientat este determinat prin urmare de două puncte (nu neapărat distincte) ale spaţiului euclidian tridimensional . Pentru segmentul orientat vom folosi în cele ce urmează notaţia . Submulţimea segmentelor orientate de forma , o vom numi „diagonala” produsului cartezian şi o vom nota .

Pentru un segment orientat punctul A se va numi originea (sau punctul de aplicaţie) iar punctul B extremitatea segmentului orientat . Segmentul orientat se va reprezenta grafic printr-o săgeată pornind din punctul A cu vârful în B (figura I.1).

Figura I.1.

1.1. Elementele caracteristice unui segment orientat

Pentru un segment orientat vom defini următoarele elemente caracteristice:

· dreapta suport: dreapta determinată de punctele A şi B;

sensul: de la A către B pe dreapta suport AB;
modulul (mărimea): distanţa euclidiană dintre punctele A şi B, notat

Definiţia 2:

Pentru două segmente orientate şi , , vom spune că au aceeaşi direcţie dacă dreptele suport AB şi CD sunt paralele sau punctele A, B, C şi D sunt colineare.

Vom nota faptul că două segmente orientate şi au aceeaşi direcţie prin .

Observaţie:

Pentru segmentele orientate aparţinând noţiunile de direcţie şi sens nu se pot defini. Evident, este caracterizată ca fiind mulţimea segmentelor orientate de modul zero.

Definiţia 3:

Două segmente orientate şi de aceeaşi direcţie, , au acelaşi sens dacă punctele B şi D sunt situate în acelaşi semiplan mărginit de dreapta AC în planul determinat de dreptele paralele AB şi CD, sau, în situaţia în care punctele A, B, C şi D sunt colineare, pe dreapta suport comună sensurile de la A la B, respectiv de la C la D, coincid.

Dacă două segmente orientate de aceeaşi direcţie nu au acelaşi sens vom spune că au sensuri opuse (sau contrarii).

Vom nota faptul că două segmente orientate şi au aceeaşi direcţie şi acelaşi sens prin . Notaţia se va utiliza pentru a nota faptul că segmentele orientate şi au aceeaşi direcţie şi sensuri opuse.

Observaţii:

1º. Se demonstrează că relaţia de paralelism definită pe mulţimea dreptelor din spaţiul euclidian tridimensional este o relaţie de echivalenţă (este reflexivă, simetrică şi tranzitivă). Clasele de echivalenţă determinate de relaţia de paralelism se numesc direcţii. Două segmente orientate au aceeaşi direcţie dacă dreptele lor suport aparţin aceleiaşi clase de echivalenţă.

2º. Se demonstrează că relaţia de „a avea acelaşi sens” definită pe mulţimea segmentelor orientate care au aceeaşi direcţie este o relaţie de echivalenţă. Există doar două clase de echivalenţă determinate de această relaţie. Prin urmare, două segmente orientate de aceeaşi direcţie au fie acelaşi sens, fie sensuri opuse.

1.2. Spaţiul liniar al segmentelor orientate legate în O

Fie un punct fixat. Vom nota prin submulţimea segmentelor orientate cu originea în O: . Pe mulţimea se poate defini o structură algebrică care în final va induce o structură pe ce modelează în mod adecvat din punct de vedere matematic fenomene descrise de mecanica teoretică.

Uneori segmentele orientate din sunt numite vectori legaţi în O. Atunci când nu există pericol de confuzie vom nota vectorii legaţi în O prin litere mici supraliniate (de ex: )

1.2.1. Adunarea vectorilor legaţi în O

Este o operaţie definită pe produsul cartezian cu valori în , notată „+”:

(I.A.1)

În definiţia de mai sus am notat prin C simetricul punctului O faţă de mijlocul segmentului .

Observaţie:

Definiţia anterioară mai este denumită şi regula paralelogramului. În situaţia în care punctele O, A, B sunt necoliniare, punctul C marchează extremitatea diagonalei OC a paralelogramului OACB (figura I.2.). Definiţia dată mai sus este utilizabilă şi în cazul în care punctele O, A şi B sunt coliniare (figura I.3.) adică atunci când paralelogramul OACB este „degenerat”. Astfel, definiţia dată asociază oricărei perechi de vectori legaţi din un vector unic determinat din .

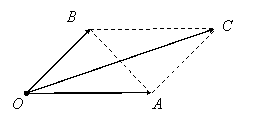Figura I.2.

Figura I.3.

Folosind definiţia (I.A.1) se demonstrează, cu uşurinţă, următoarele proprietăţi:

(a1) ;

(a2) astfel încât :

Vectorul se numeşte vector nul.

(a3) , astfel încât:

Dacă , atunci unde este simetricul lui A faţă de O. este un segment orientat cu aceeaşi direcţie şi modul ca şi vectorul , dar de sens opus.

(a4) .

În conformitate cu proprietăţile (a1)-(a4) rezultă că mulţimea vectorilor legaţi în O, , împreună cu operaţia de adunare definită prin relaţia (I.A.1) formează o structură algebrică de grup abelian.

1.2.2. Înmulţirea vectorilor legaţi în O cu scalari reali

Este o operaţie definită pe produsul cartezian cu valori în , notată „”:

(I.A.2)

Pentru a caracteriza univoc vectorul din definiţia (I.A.2) este suficient a-i preciza direcţia, sensul şi modulul:

· direcţia: direcţia vectorului ;

sensul: acelaşi cu dacă ;

opus lui dacă ;

modulul (mărimea): .

Pentru a elimina ambiguităţile definim:

Cu precizările de mai sus, definiţia (I.A.2) asociază univoc oricărei perechi din , formată dintr-un scalar real şi un vector legat în O, un vector legat din .

Folosind definiţia (I.A.2) se probează următoarele proprietăţi:

(i1) ;

(i2) ;

(i3) ;

(i4) .

Observaţie:

Folosind definiţia (I.A.2) şi proprietatea (a3) avem:

(I.A.3)

Uneori, pentru simplificarea scrierii, se foloseşte convenţia , omiţându-se punctul care desemnează înmulţirea unui vector legat din cu un scalar real. Relaţia precedentă se mai scrie sub forma:

(I.A.4)

omiţând scrierea scalarului -1.

Pe această cale se poate defini operaţia de „scădere” sau „diferenţa” a doi vectori din :

(I.A.5)

Astfel capătă sens scrieri de forma: definite ca operaţii cu vectori legaţi din .

Proprietăţile (i1)-(i4) ale operaţiei (I.A.2) şi faptul că este grup abelian demonstrează că mulţimea a vectorilor legaţi în O împreună cu operaţiile definite prin relaţiile (I.A.1) şi (I.A.2) formează un spaţiu liniar (vectorial) peste corpul numerelor reale . Acest -spaţiu liniar poartă numele de spaţiul liniar (vectorial) al vectorilor legaţi în punctul O. Uneori, se mai numeşte şi spaţiul liniar (vectorial) tangent în punctul O la .

1.2.3. Subspaţii liniare remarcabile

Vom spune că submulţimea este subspaţiu liniar propriu al lui dacă este închisă la operaţiile definite prin relaţiile (I.A.1) şi (I.A.2), adică păstrează ereditar proprietăţile de -spaţiu liniar.