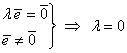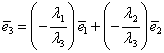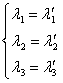Teorema 2 mai poate fi formulată şi în
modul următor: orice vector nenul din ![]() generează întreg spaţiul vectorial
generează întreg spaţiul vectorial ![]() .
.
De asemenea are loc implicaţia:
|
|
(I.A.11) |
Se spune că vectorul ![]() este liniar independent.
Astfel mulţimea
este liniar independent.
Astfel mulţimea ![]() ,
,
![]() ,
, ![]() , este liniar
independentă şi generează subspaţiul liniar
, este liniar
independentă şi generează subspaţiul liniar ![]() . Ea se numeşte bază în
. Ea se numeşte bază în ![]() . Cum subspaţiul
liniar
. Cum subspaţiul
liniar ![]() admite
o bază formată dintr-un singur vector, se spune că
admite
o bază formată dintr-un singur vector, se spune că ![]() este un subspaţiu liniar de
dimensiune 1 peste corpul numerelor reale
este un subspaţiu liniar de
dimensiune 1 peste corpul numerelor reale ![]() şi se scrie:
şi se scrie:
|
|
(I.A.12) |
Subspaţiul liniar ![]() se numeşte dreaptă vectorială.
se numeşte dreaptă vectorială.
1.2.3.2. Planul vectorial în ![]()
Fie ![]() un plan ce trece prin punctul
un plan ce trece prin punctul ![]() şi submulţimea lui
şi submulţimea lui ![]() :
:
|
|
(I.A.13) |
Mulţimea ![]() este formată din vectorii legaţi în O
ale căror drepte suport sunt conţinute în planul
este formată din vectorii legaţi în O
ale căror drepte suport sunt conţinute în planul ![]() (figura I.5).
(figura I.5).
Evident, ![]() , deci, în conformitate cu Teorema 1,
, deci, în conformitate cu Teorema 1,
![]() este un
subspaţiu liniar propriu al lui
este un
subspaţiu liniar propriu al lui ![]() .
.
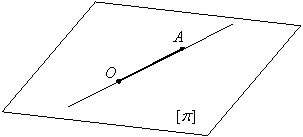
Figura I.5.
Teorema 3:
Fie ![]() ,
, ![]() . Oricare ar fi
. Oricare ar fi ![]() există
există ![]() astfel încât:
astfel încât:
|
|
(I.A.14) |
Demonstraţie:
Fie ![]() şi
şi ![]() dreptele suport ale vectorilor legaţi
dreptele suport ale vectorilor legaţi ![]() , respectiv
, respectiv ![]() (figura I.6). Avem
(figura I.6). Avem ![]() şi
şi ![]() .
.
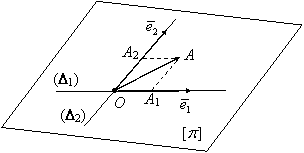 |
Figura I.6.
Notăm ![]() şi fie punctele
şi fie punctele ![]() .
. ![]() se află la intersecţia dreptei suport
se află la intersecţia dreptei suport ![]() cu paralela dusă prin A
la dreapta
cu paralela dusă prin A
la dreapta ![]() .
Analog, punctul
.
Analog, punctul ![]() este
intersecţia dintre dreapta
este
intersecţia dintre dreapta ![]() şi paralela prin A la dreapta
şi paralela prin A la dreapta ![]() . Deoarece patrulaterul
. Deoarece patrulaterul
![]() este
paralelogram, rezultă:
este
paralelogram, rezultă:
|
|
(I.A.15) |
Pe dreptele vectoriale ![]() şi
şi ![]() avem, în conformitate cu Teorema
2:
avem, în conformitate cu Teorema
2:
|
|
(I.A.16) |
|
|
(I.A.17) |
Din relaţiile (I.A.15), (I.A.16) şi (I.A.17) rezultă (I.A.14). ♦
Relaţia (I.A.14) demonstrează că vectorii ![]() şi
şi ![]() generează subspaţiul liniar
generează subspaţiul liniar ![]() .
.
Teorema 4:
Fie ![]() ,
, ![]() . Are loc implicaţia:
. Are loc implicaţia:
|
|
(I.A.18) |
Demonstraţie:
Presupunem, de exemplu, ![]() . Din (I.A.18) rezultă:
. Din (I.A.18) rezultă:
|
|
(I.A.19) |
Relaţia (I.A.19) contrazice ipoteza ![]() . Analog rezultă
. Analog rezultă ![]() . ♦
. ♦
Teorema 4 ne asigură că doi vectori ![]() şi
şi ![]() ,
, ![]() , sunt liniar independenţi.
, sunt liniar independenţi.
Mulţimea ![]() , cu
, cu ![]() ,
, ![]() , este formată din vectori legaţi din
, este formată din vectori legaţi din ![]() liniar independenţi
care generează subspaţiul liniar
liniar independenţi
care generează subspaţiul liniar ![]() . Mulţimea
. Mulţimea ![]() se numeşte bază în
se numeşte bază în ![]() . Cum subspaţiul liniar
. Cum subspaţiul liniar
![]() admite o
bază formată din doi vectori, se spune că
admite o
bază formată din doi vectori, se spune că ![]() este un subspaţiu liniar de dimensiune 2
peste corpul numerelor reale
este un subspaţiu liniar de dimensiune 2
peste corpul numerelor reale ![]() şi se scrie:
şi se scrie:
|
|
(I.A.20) |
Subspaţiul liniar ![]() se numeşte plan vectorial.
se numeşte plan vectorial.
Observaţii:
1º.
Folosind Teorema 4 se demonstrează cu uşurinţă că scrierea (I.A.14) din Teorema
2 este unică. Numerele reale unic determinate ![]() din relaţia (I.A.14) se numesc componentele vectorului
din relaţia (I.A.14) se numesc componentele vectorului
![]() în baza
în baza ![]() . O bază în planul
vectorial
. O bază în planul
vectorial ![]() poate
fi formată din oricare doi vectori necoliniari din
poate
fi formată din oricare doi vectori necoliniari din ![]() .
.
2º.
Fie ![]() un plan
ce trece prin punctul
un plan
ce trece prin punctul ![]() şi
şi ![]() ,
, ![]() două drepte distincte conţinute în planul
două drepte distincte conţinute în planul
![]() concurente
în punctul O. Considerăm planul vectorial
concurente
în punctul O. Considerăm planul vectorial ![]() şi dreptele vectoriale
şi dreptele vectoriale ![]() , respectiv
, respectiv![]() . Teorema 3 şi observaţia anterioară ne
asigură că
. Teorema 3 şi observaţia anterioară ne
asigură că ![]() există
unic determinaţi vectorii
există
unic determinaţi vectorii ![]() şi
şi ![]() astfel încât:
astfel încât:
|
|
(I.A.21) |
Deoarece ![]() se spune că planul vectorial
se spune că planul vectorial ![]() este suma directă a
dreptelor vectoriale
este suma directă a
dreptelor vectoriale ![]() şi
şi ![]() şi se scrie:
şi se scrie:
|
|
(I.A.22) |
1.2.4. Baze în spaţiul liniar al vectorilor legaţi în O
După metodologia folosită în cazul subspaţiilor
vectoriale proprii definite anterior vom căuta în ![]() un sistem de vectori care să fie liniar
independenţi şi să genereze spaţiul liniar
un sistem de vectori care să fie liniar
independenţi şi să genereze spaţiul liniar ![]() .
.
Fie ![]() trei vectori legaţi nenuli din
trei vectori legaţi nenuli din ![]() ale căror drepte
suport, notate
ale căror drepte
suport, notate ![]() ,
,
![]() şi
şi ![]() , sunt necoplanare. În
acest caz vectorii
, sunt necoplanare. În
acest caz vectorii ![]() ,
se numesc necoplanari (figura I.7).
,
se numesc necoplanari (figura I.7).
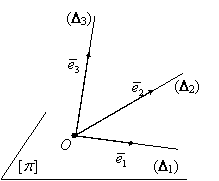 |
Figura I.7.
Teorema 5:
Fie ![]() trei vectori necoplanari. Oricare ar fi
trei vectori necoplanari. Oricare ar fi ![]() există
există ![]() astfel încât:
astfel încât:
|
|
(I.A.23) |
Demonstraţie:
Dacă ![]() se observă că relaţia (I.A.23) este
satisfăcută cu
se observă că relaţia (I.A.23) este
satisfăcută cu ![]() .
În continuare presupunem,
.
În continuare presupunem, ![]() (figura I.8).
(figura I.8).
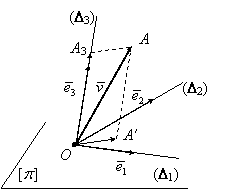 |
Figura I.8.
Fie ![]() planul determinat de dreptele concurente
distincte
planul determinat de dreptele concurente
distincte ![]() şi
şi
![]() . Notăm cu
. Notăm cu ![]() punctul de intersecţie
al planului
punctul de intersecţie
al planului ![]() cu
paralela dusă prin punctul A la dreapta
cu
paralela dusă prin punctul A la dreapta ![]() . Notăm cu A3 punctul de
intersecţie al dreptei
. Notăm cu A3 punctul de
intersecţie al dreptei ![]() cu paralela dusă prin punctul A la
dreapta
cu paralela dusă prin punctul A la
dreapta ![]() . În
planul determinat de dreptele paralele
. În
planul determinat de dreptele paralele ![]() şi
şi ![]() avem:
avem:
|
|
(I.A.24) |
Conform teoremei 3, în planul vectorial ![]() putem scrie
descompunerea:
putem scrie
descompunerea:
|
|
(I.A.25) |
Pe dreapta vectorială ![]() avem, conform teoremei 2:
avem, conform teoremei 2:
|
|
(I.A.26) |
Din relaţiile (I.A.24), (I.A.25) şi (I.A.26) rezultă (I.A.23).
♦
Prin urmare, vectorii necoplanari ![]() , generează
spaţiul liniar
, generează
spaţiul liniar ![]() . Se mai spune că vectorii
. Se mai spune că vectorii ![]() , formează un sistem
de generatori pentru
, formează un sistem
de generatori pentru ![]() .
.
Teorema 6:
Fie ![]() , trei vectori legaţi din
, trei vectori legaţi din ![]() necoplanari. Are loc
implicaţia:
necoplanari. Are loc
implicaţia:
|
|
(I.A.27) |
Demonstraţie:
Presupunem ![]() . Din ipoteza relaţiei (I.A.27) se obţine:
. Din ipoteza relaţiei (I.A.27) se obţine:
|
|
(I.A.28) |
Relaţia (I.A.28) arată că ![]() , ceea ce contrazice ipoteza
necoplanarităţii vectorilor legaţi
, ceea ce contrazice ipoteza
necoplanarităţii vectorilor legaţi ![]() . Rezultă deci că
. Rezultă deci că ![]() . Analog se demonstrează că
. Analog se demonstrează că ![]() . ♦
. ♦
Prin urmare, vectorii necoplanari ![]() , sunt liniar
independenţi.
, sunt liniar
independenţi.
Teorema 7:
În ipoteza necoplanarităţii vectorilor ![]() , scrierea (I.A.23)
dată de teorema 5 este unică.
, scrierea (I.A.23)
dată de teorema 5 este unică.
Demonstraţie:
Presupunem că ![]() , astfel încât:
, astfel încât:
|
|
(I.A.29) |
Din relaţiile (I.A.23) şi (I.A.29) rezultă:
|
|
(I.A.30) |
ţinând cont de teorema 6, din (I.A.30) se obţine:
|
|
(I.A.31) |
Relaţia (I.A.31) demonstrează teorema. ♦