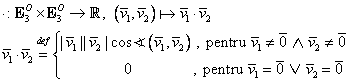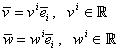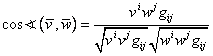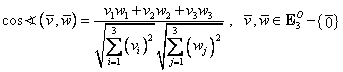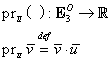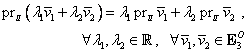Fie mulţimea  cu , vectori legaţi necoplanari. Această mulţime este formată din vectori legaţi în O liniar independenţi (teorema 6) ce constituie un sistem de generatori pentru spaţiul liniar  (teorema 5). O astfel de mulţime se numeşte bază în spaţiul liniar . Întrucât baza  are trei elemente se spune că dimensiunea spaţiului liniar  peste corpul numerelor reale este 3 şi se scrie:

(I.A.32)

 

Observaţii:

            1º. Numerele reale , , din relaţia (I.A.23), unic determinate, se numesc componentele vectorului legat  în baza . O bază în  este formată din oricare trei vectori necoplanari.

            2º. Fie , , trei drepte necoplanare, concurente în punctul . Considerăm , , dreptele vectoriale corespunzătoare. Din cele prezentate mai sus (teoremele 5 şi 6) rezultă că  există, unic determinaţi, vectorii , , astfel încât:

(I.A.33)

            În acest caz se spune că spaţiul liniar  este suma directă a dreptelor vectoriale , , şi se scrie:

(I.A.34)

            Vectorul legat  din relaţia (I.A.33) reprezintă diagonala paralelipipedului construit cu vectorii legaţi  ca muchii (figura I.9).

 

 

 

 

 

 

 

 

 

 

 

 

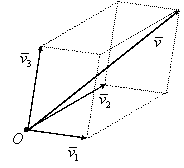Figura I.9.

 

            3º. Fie  şi  un plan, respectiv o dreaptă, care trec prin punctul O astfel încât  (figura I.10). Considerăm  un vector legat în O,  şi . Notăm cu  punctul de intersecţie al planului  cu paralela dusă prin punctul A la dreapta  şi cu  punctul de intersecţie al dreptei  cu paralela dusă prin punctul A la dreapta .

            În planul determinat de dreptele paralele  şi  avem . Cu notaţiile  şi , avem , .

 

 

 

 

 

 

 

 

 

 

 

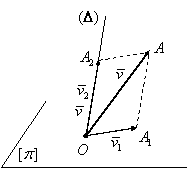Figura I.10.

            Din cele prezentate mai sus rezultă că  există, unic determinaţi, vectorii  şi  astfel încât . Am demonstrat astfel că spaţiul liniar  este suma directă a dreptei vectoriale  cu planul vectorial :

(I.A.35)

 

            4º. Fiind dată baza  din , dacă dreptele suport ale vectorilor bazei sunt reciproc perpendiculare, baza se numeşte bază ortogonală. Vom scrie acest lucru sub forma . Dacă, în plus, baza este formată din versori (vectori de modul 1) atunci baza se numeşte bază ortonormată.

 

            5º. Fie  o bază în  şi  un vector legat în O arbitrar. Notând componentele vectorului  în baza  cu indici superiori, descompunerea unică (I.A.23) a vectorului legat  în baza considerată devine:

,

(I.A.36)

            Din raţiuni legate de concizia scrierii, relaţia (I.A.36) se scrie în forma:

(I.A.36')

utilizând aşa numita regulă de sumare a indicilor muţi:

 

 

Această regulă va fi folosită în cele ce urmează, în afara situaţiilor care vor fi menţionate în mod expres. Dacă nu se va specifica contrariul, “indicii muţi” vor lua toate valorile din mulţimea .

 

1.3. Operaţii cu vectori legaţi din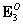

            Necesităţi legate de calculul efectiv al coeficienţilor unui vector legat într-o bază dată, precum şi cele impuse de posibilitatea exprimării în formă concisă a unor proprietăţi intrinseci, au condus la introducerea unor noi operaţii în . Definiţiile şi câteva dintre proprietăţile acestora vor fi trecute în revistă în continuare.

 

1.3.1. Produsul scalar al vectorilor legaţi din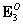

            Este o operaţie, notată cu „”, care asociază oricărei perechi de vectori legaţi din  un număr real:

(I.A.37)

            În relaţia (I.A.37) am notat cu  unghiul dintre semidreptele suport ale vectorilor legaţi nenuli  şi , unghi care ia valori în intervalul . Au loc echivalenţele:

	(I.A.38)
	(I.A.39)

            În cazul produsului scalar al unui vector legat  cu el însuşi se foloseşte notaţia:

(I.A.40)

            Folosind definiţia (I.A.37) se demonstrează următoarele proprietăţi:

(s1)      ;

(s2)      ;

(s3)      ;

(s4)      .

 

            Fie  o bază în  şi , respectiv , doi vectori legaţi arbitrari din . Au loc descompunerile unice:

(I.A.41)

            Cu proprietăţile (s1)-(s3) şi relaţiile (I.A.41), rezultă expresia produsului scalar  scrisă, utilizând regula de sumare a indicilor muţi, sub forma:

(I.A.42)

            Folosind notaţia:

(I.A.43)

relaţia (I.A.42) devine:

(I.A.44)

            În particular, pentru  din (I.A.44) rezultă:

(I.A.45)

            Conform definiţiei (I.A.37) avem , de unde cu proprietatea (s4) se obţine:

(I.A.46)

            ţinând cont de relaţiile (I.A.45) şi (I.A.46) rezultă:

(I.A.47)

            De asemenea, din definiţia (I.A.37) şi relaţiile (I.A.44) şi (I.A.47), dacă vectorii legaţi  şi  sunt nenuli, , atunci cosinusul unghiului format de cei doi vectori este dat de:

(I.A.48)

 

            Din definiţia (I.A.37) rezultă că produsul scalar a doi vectori legaţi ortogonali este nul.

 

            Introducând convenţia că vectorul legat nul, , este ortogonal pe orice vector din  se poate enunţa următoarea teoremă ce caracterizează vectorii legaţi ortogonali din :

 

            Teorema 8:

            Are loc echivalenţa:

(I.A.49)

 

Observaţii:

            1º. În situaţia în care baza  este ortonormată se obţine:

(I.A.50)

unde  notează simbolul lui Kronecker definit prin:

(I.A.51)

            În cazul unei baze ortonormate indicii componentelor vectorilor din relaţiile (I.A.41) se scriu jos:

(I.A.52)

astfel că relaţiile (I.A.44), (I.A.47) şi (I.A.48) devin:

	(I.A.53)
	(I.A.54)
	(I.A.55)

 

            2º. Fie  o dreaptă orientată ce trece prin punctul O, orientare dată de versorul , (figura I.11).

            Dat fiind vectorul legat , se numeşte proiecţia vectorului legat  pe dreapta orientată  numărul real:

(I.A.56)

 

 

 

Figura I.11.

 

            3º. Fie  o dreaptă arbitrară ce trece prin punctul O. Dat fiind vectorul legat , se numeşte proiecţia vectorială a vectorului legat  pe dreapta  vectorul legat:

(I.A.57)

unde  este unul din cei doi versori ai dreptei  (figura I.12). Se observă că relaţia (I.A.57) rămâne invariantă dacă înlocuim versorul  cu versorul .

 

 

 

Figura I.12.

 

            4º. Fie  un versor legat în O, . Numim proiecţia vectorului arbitrar  pe versorul  aplicaţia:

(I.A.58)

            Pe baza proprietăţilor produsului scalar se demonstrează că aplicaţia (I.A.58) este -liniară:

(I.A.59)

 

            De asemenea se observă că au loc echivalenţele:

(I.A.60)

---