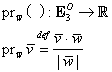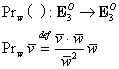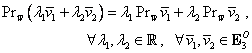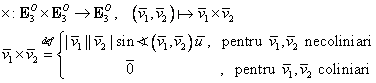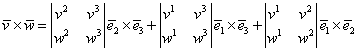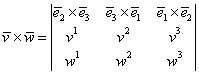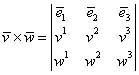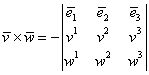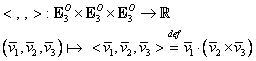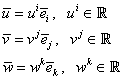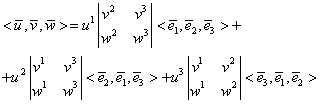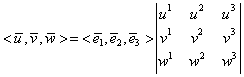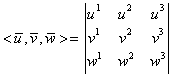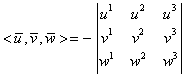Dacă  arbitrar, atunci  este un versor liber, . Proiecţia vectorului  pe vectorul  este aplicaţia:

(I.A.61)

 

            Evident, proprietăţile (I.A.59) şi (I.A.60) se păstrează şi pentru aplicaţia (I.A.61).

 

            5º. Definim proiecţia vectorială a vectorului  pe vectorul  fixat aplicaţia:

(I.A.62)

 

            Se observă că pentru  fixat avem:

,

(I.A.63)

de unde rezultă că şi aplicaţia (I.A.63) este -liniară:

(I.A.64)

 

1.3.2. Produsul vectorial al vectorilor legaţi din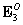

            Produsul vectorial este o operaţie notată cu „”, care asociază oricărei perechi de vectori legaţi din  un vector din :

(I.A.65)

 

            În definiţia (I.A.65), dacă cel puţin unul dintre cei doi vectori este nul sau cei doi vectori au aceeaşi dreaptă suport produsul vectorial este prin definiţie vectorul legat nul .

            Dacă vectorii  şi  sunt necoliniari, în definiţia de mai sus  reprezintă un versor normal la planul determinat de dreptele suport (concurente în punctul O) ale celor doi vectori necoliniari.

            Sensul versorului  este dat de sensul de înaintare al unui burghiu drept în ipoteza suprapunerii vectorului legat  peste vectorul legat  prin micşorarea progresivă a unghiului dintre cei doi vectori legaţi (unghi definit anterior) (figura I.13).

 

 

 

 

 

 

 

 

 

 

 

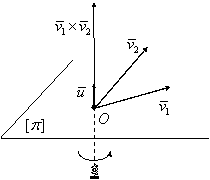Figura I.13.

 

            Regula după care se determină sensul versorului  (şi implicit sensul vectorului ) este denumită uneori regula burghiului drept.

 

Observaţii:

            1º. Definiţia produsului vectorial presupune o anumită „orientare” a spaţiului euclidian tridimensional. Aşa cum a fost definită mai sus noţiunea de produs vectorial face apel la „experienţa de viaţă” a speciei umane în spaţiul fizic tridimensional (rotirea unui burghiu, a unui tirbuşon, etc.) modelat matematic de .

            În anumite manuale regula burghiului drept este înlocuită cu aşa numita regula mâinii stângi care face însă apel la anumite caracteristici anatomice ale speciei umane.

 

            Pentru scopurile prezentei lucrări definiţia dată operaţiei produs vectorial (care face apel şi la intuiţie) este suficientă. Atenţionăm însă cititorul că în acest caz, ca şi în cazul „obiectelor matematice” mai cuprinzătoare (de exemplu cazul „varietăţilor diferenţiabile”) noţiunea de „orientare” trebuie definită riguros, fără ambiguităţi.

 

            2º. Din definiţia (I.A.62) rezultă:

(I.A.66)

 

            Modulul produsului vectorial a doi vectori legaţi în O este egal cu aria paralelogramului construit cu vârful în punctul O având ca laturi vectorii legaţi  şi  (figura I.14):

(I.A.67)

             se mai numeşte uneori aria orientată a paralelogramului OACB.

 

 

 

 

Figura I.14.

 

            Din definiţie, folosind raţionamente simple, rezultă următoarele proprietăţi ale produsului vectorial:

(v1)      ;

(v2)      ;

(v3)      .

 

            Fie  o bază în  şi , , doi vectori legaţi arbitrari din  daţi prin relaţiile (I.A.41) se obţine:

(I.A.68)

            Din relaţia (I.A.68), folosind proprietatea (v1) se obţine:

(I.A.69)

relaţie echivalentă cu

(I.A.70)

            Relaţia (I.A.70) se poate scrie succint sub forma unui determinant simbolic:

(I.A.71)

            Scrierile (I.A:70) şi (I.A.71) sunt echivalente cu condiţia ca „determinantul” (I.A.71) să se dezvolte doar după elementele primei linii.

 

            În situaţia în care baza  este ortonormată există doar două situaţii distincte, ilustrate în figura I.15.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

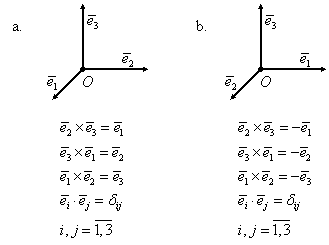Figura I.15.

 

            În cazul prezentat în figura I.15.a. baza  se numeşte ortonormată dreaptă, iar în cazul din figura I.15.b. baza se numeşte ortonormată stângă.

            În cazul bazelor ortonormate drepte relaţia (I.A.71) devine:

(I.A.72)

iar în cazul bazelor ortonormate stângi avem:

(I.A.73)

 

            Prin definiţia (I.A.65) produsul vectorial a doi vectori legaţi coliniari din  este vectorul nul din . Introducând convenţia că vectorul nul  este coliniar cu orice vector legat din  se obţine următoarea teoremă de caracterizare a vectorilor legaţi coliniari din :

 

            Teorema 9:

            Are loc echivalenţa:

(I.A.74)

 

1.3.3. Produsul mixt al vectorilor legaţi din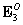

            Produsul mixt, notat „”, este o operaţie care asociază oricărui triplet de vectori legaţi din  un număr real:

(I.A.75)

            Folosind definiţia (I.A.75) se constată uşor că dacă cel puţin unul dintre cei trei vectori este vectorul legat nul din  atunci produsul mixt este zero. De asemenea, dacă cei trei vectori legaţi sunt nenuli dar coplanari, produsul lor mixt este de asemenea nul.

 

            Fie acum trei vectori legaţi din  nenuli şi necoplanari, . Folosind definiţia produsului scalar (I.A.37) din relaţia (I.A.75) se obţine:

(I.A.76)

            Fie  paralelipipedul cu un vârf în punctul  având ca muchii ce pleacă din vârful O vectorii . Sunt posibile două situaţii prezentate în figurile I.16 şi I.17.

 

 

 

 

 

 

 

 

 

 

 

 

 

Figura I.16.

 

 

Figura I.17.

 

            Cu observaţia (I.A.67) făcută în cazul produsului vectorial avem:

(I.A.77)

            Notând cu h înălţimea paralelipipedului  se obţine:

(I.A.78)

            În relaţia (I.A.78), dacă  atunci se ia semnul plus (caz prezentat în figura I.16); semnul minus se ia dacă  (figura I.17).

            Din relaţiile (I.A.76), (I.A.77) şi (I.A.78) rezultă:

(I.A.79)

            Dacă relaţia (I.A.79) are loc cu semnul plus, atunci  şi sistemul de vectori necoplanari  luaţi în această ordine se spune că este orientat drept.

            Dacă relaţia (I.A.79) are loc cu semnul minus, atunci  şi sistemul de vectori necoplanari  luaţi în această ordine se spune că este orientat stâng.

 

            Cu definiţia (I.A.75) şi observaţiile de mai sus, folosind proprietăţile produsului scalar şi cele ale produsului vectorial, se demonstrează următoarele proprietăţi ale produsului mixt:

(m1)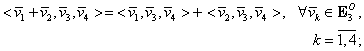    

(m2)    

unde 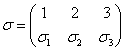 este o permutare a mulţimii , iar  notează signatura permutării ;

(m3)     .

            Din proprietăţile (m1)-(m3) rezultă că produsul mixt este o operaţie liniară şi omogenă în raport cu oricare din cele trei argumente. Proprietatea (m2) poartă numele de comutativitate ciclică.

 

            Fie  o bază în spaţiul liniar  şi  trei vectori legaţi arbitrari:

(I.A.80)

            Cu relaţia (I.A.70) şi proprietăţile (m1) şi (m3) se obţine:

(I.A.81)

relaţie echivalentă conform proprietăţii (m2) cu:

(I.A.82)

 

            Dacă baza  este o bază ortonormată dreaptă, atunci  şi relaţia (I.A.82) devine:

(I.A.83)

            Dacă baza  este o bază ortonormată stângă, atunci  şi relaţia (I.A.82) devine:

(I.A.84)

 

            Cu observaţiile anterioare se poate enunţa următoarea teoremă de caracterizare a bazelor din spaţiul liniar :

 

            Teorema 10:

            Fie  trei vectori legaţi din . Are loc echivalenţa:

bază în

(I.A.85)

 

Observaţii:

            1º. Dacă avem o bază  în spaţiul liniar  şi , baza  se numeşte bază orientată drept. Dacă  baza  se numeşte bază orientată stâng.

 

            2º. Am demonstrat, prin teorema 6, că oricare trei vectori legaţi din  necoplanari sunt liniar independenţi. Evident, trei vectori legaţi din  coplanari sunt liniar dependenţi (cel puţin unul dintre ei se scrie ca o combinaţie liniară de ceilalţi doi), vectorii aparţinând aceluiaşi plan vectorial.

Admiţând, prin convenţie, că vectorul legat nul  este coplanar cu oricare doi vectori necoliniari, rezultă că produsul mixt al vectorilor legaţi din  caracterizează liniar independenţa sau liniar dependenţa a trei vectori legaţi. Astfel, au loc echivalenţele:

- liniar dependenţi     - liniar independenţi

(I.A.86)

 

---