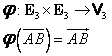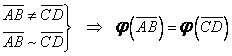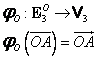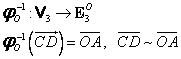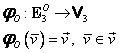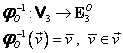2. Mulţimea vectorilor liberi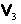

            Folosind construcţiile anterioare vom introduce noţiunea de vector liber indispensabilă modelării matematice a fenomenelor fizice. Mulţimea vectorilor liberi va fi înzestrată apoi cu o structură algebrică adecvată ce permite dezvoltarea aşa-numitului calcul vectorial.

 

2.1. Vectori liberi

            Pe mulţimea segmentelor orientate se poate introduce o relaţie binară numită relaţia de echipolenţă:

 

            Definiţia 5:

            Două segmente orientate,  se numesc echipolente dacă mijlocul segmentului  coincide cu mijlocul segmentului ,  (figura I.18).

 

 

 

 

 

 

 

 

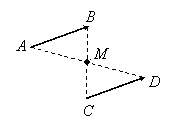Figura I.18.

 

Observaţii:

            1º. Conform definiţiei, toate segmentele orientate de forma  sunt echipolente.

 

            2º. Segmentele orientate ,  sunt echipolente dacă patrulaterul  este paralelogram (eventual degenerat). Paralelogramul  este considerat degenerat dacă segmentele orientate  şi  au aceeaşi dreaptă suport (figura I.19).

 

 

 

 

 

 

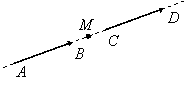Figura I.19.

 

            3º. Segmentele orientate ce au dreptele suport paralele (sau confundate) se numesc segmente orientate cu aceiaşi direcţie. Din definiţia 5 rezultă că două segmente orientate echipolente au aceiaşi direcţie.

 

            4º. Din definiţia de mai sus rezultă, de asemenea, că două segmente orientate echipolente au acelaşi sens şi acelaşi modul. Prin urmare, segmentele orientate echipolente au aceiaşi direcţie, acelaşi sens şi acelaşi modul.

 

            5º. Relaţia de echipolenţă, aşa cum a fost definită mai sus, este o submulţime a produsului cartezian .

 

            Vom nota faptul că două segmente orientate, ,  sunt echipolente prin . Are loc echivalenţa (de fapt notaţiile echivalente):

(I.A.87)

 

            Teorema 11:

            Relaţia de echipolenţă a segmentelor orientate este o relaţie de echivalenţă.

 

 

 

            Demonstraţie:

            Folosind definiţia şi proprietăţi de geometrie elementară se arată că relaţia de echipolenţă este:

            reflexivă:        ;

            simetrică:

;

            tranzitivă:

.

♦

 

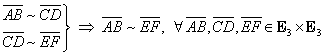            Teorema precedentă permite partiţionarea mulţimii segmentelor orientate  în clase de echivalenţă. Într-o anumită clasă de echivalenţă se găsesc toate segmentele orientate echipolente între ele. În conformitate cu observaţia 1º elementele aparţinând  constituie o clasă de echivalenţă. În afară de această clasă, toate celelalte clase de echivalenţă conţin segmente orientate de aceiaşi direcţie, acelaşi sens şi acelaşi modul.

 

            Vom nota prin  clasa de echivalenţă determinată de segmentul orientat :

(I.A.88)

 

            În conformitate cu proprietatea de reflexivitate a relaţiei de echipolenţă, această clasă este nevidă (conţine cel puţin segmentul orientat ). Au loc următoarele echivalenţe:

	(I.A.89)
	(I.A.90)

 

            Mulţimea ce are ca elemente clasele de echivalenţă (în raport cu relaţia de echipolenţă a segmentelor orientate) se numeşte mulţimea factor a segmentelor orientate  în raport cu relaţia de echipolenţă „” şi se notează cu .

 

            Definiţia 6:

            Se numeşte mulţimea vectorilor liberi din spaţiul euclidian tridimensional , notată , mulţimea factor a segmentelor orientate  în raport cu relaţia de echipolenţă „”:

(I.A.91)

 

Observaţii:

            1º. Un vector liber  nu este un segment orientat, ci o clasă de echivalenţă (o mulţime de segmente orientate echipolente).

            Segmentul orientat  dacă şi numai dacă . În acest caz, segmentul orientat  se numeşte reprezentantul în punctul  al vectorului liber .

 

            2º. Dat fiind punctul , orice vector liber  din  are un reprezentant unic în  (vectorul legat din  care are aceeaşi direcţie, acelaşi sens şi acelaşi modul cu ). Reprezentantul în  al clasei de echivalenţă determinată de  este vectorul legat nul din .

 

            3º. Aplicaţia ce asociază oricărui segment orientat din  clasa de echivalenţă (vectorul liber) din  căreia îi aparţine:

(I.A.92)

este o surjecţie numită surjecţie canonică.

            Într-adevăr, orice vector liber are cel puţin un reprezentant în , deci aplicaţia (I.A.92) este surjectivă.

            Aplicaţia (I.A.92) nu este injectivă. Într-adevăr, fie  două segmente orientate din  distincte echipolente. Are loc implicaţia:

(I.A.93)

 

            Restricţia aplicaţiei  la , notată :

(I.A.94)

este injectivă (conform observaţiei 2º de mai sus) şi surjectivă, deci este bijectivă. Această aplicaţie asociază oricărui vector legat din  vectorul liber (unic) din  căruia îi aparţine.

            Inversa aplicaţiei (I.A.94):

(I.A.95)

asociază oricărui vector liber din  un reprezentant (unic) din  (un vector legat în O).

 

            4º. Pentru unificarea scrierii vom nota vectorii liberi din  cu litere latine mici supraliniate cu o săgeată (ex. ). Vectorii legaţi din  (, fixat) vor fi notaţi ca şi până acum, cu litere latine mici supraliniate (ex. ).

            Cu aceste convenţii bijecţiile (I.A.94) şi (I.A.95) se scriu:

(I.A.96)

respectiv:

(I.A.97)

 

            Cu ajutorul bijecţiilor (I.A.94) şi (I.A.95) structura de spaţiu liniar real a lui  se poate „transporta” pe mulţimea vectorilor liberi .

 

2.2. Spaţiul liniar al vectorilor liberi

            Vectorii liberi fiind clase de echivalenţă (mulţimi de segmente orientate echipolente) operaţiile pe această mulţime se vor defini prin intermediul unor reprezentanţi din . Pentru ca definiţiile să fie consistente trebuie verificat, de fiecare dată, că ele nu depind de reprezentanţii aleşi.

 

2.2.1. Adunarea vectorilor liberi

            Adunarea vectorilor liberi este o operaţie notată „+” ce asociază oricărei perechi de vectori liberi, în mod unic, un alt vector liber:

(I.A.98)

 

            Din relaţia (I.A.98) rezultă că pentru a aduna doi vectori liberi se procedează astfel:

 

 

·        se fixează un punct arbitrar ;

·        se consideră vectorii legaţi în O,  şi , reprezentanţi ai vectorilor liberi , respectiv ;

·        se efectuează suma ;

·        prin definiţie, vectorul liber  este clasa de echivalenţă ce are ca reprezentant în O pe .

 

            Operaţia definită prin relaţia (I.A.98) nu depinde de alegerea punctului . Considerăm un punct  diferit de punctul O şi fie  şi  reprezentanţii în  ai vectorilor liberi , respectiv  (figura I.20).

 

 

 

 

 

 

 

 

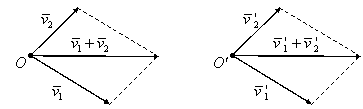Figura I.20

 

 

            Avem:

(I.A.99)

deoarece .

            Din relaţiile (I.A.99), folosind definiţiile adunării vectorilor legaţi în punctele O, respectiv O', şi proprietăţi de geometrie elementară, rezultă:

(I.A.100)

            Relaţia (I.A.100) arată că vectorii legaţi  şi  aparţin aceleiaşi clase de echivalenţă în raport cu relaţia de echipolenţă, deci:

		(I.A.101)

 

            Relaţia (I.A.101) demonstrează că adunarea vectorilor liberi, definită prin relaţia (I.A.98), nu depinde de reprezentanţii aleşi (nu depinde de alegerea punctului O).

 

            Observaţiile anterioare permit transcrierea proprietăţilor adunării vectorilor legaţi (a1)-(a4) în cazul adunării vectorilor liberi:

(A1)     ;

(A2)     astfel încât  ,  ;

            Vectorul , se numeşte vector nul.

(A3)     astfel încât:   ;

            Dacă , atunci .

(A4)     .

 

            Proprietăţile (A1)-(A4) arată că mulţimea vectorilor liberi, , împreună cu operaţia de adunare definită prin relaţia (I.A.98) formează o structură algebrică de grup abelian.

 

---