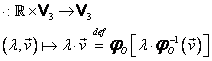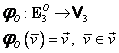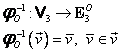Lecţia 1

Observaţii:

1º. Adunarea vectorilor liberi se defineşte uneori folosind aşa-numita regulă a triunghiului. Fie şi doi vectori liberi oarecare şi A un punct fixat arbitrar în spaţiu. Considerăm şi reprezentanţii celor doi vectori liberi în punctele , respectiv (figura I.21). Se defineşte:

(I.A.102)

Se constată, fără dificultate, că definiţia (I.A.102) nu depinde de punctul A şi că definiţiile (I.A.98) şi (I.A.102) sunt echivalente.

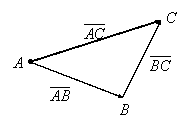Figura I.21.

Figura I.21 justifică denumirea de regulă a triunghiului dată definiţiei (I.A.102) a adunării vectorilor liberi.

Deseori figura I.21 se desenează în mod abuziv ca în figura I.22 deşi vectorii liberi sunt clase de echivalenţă şi nu pot fi reprezentate grafic. În figura I.22 se desenează doar reprezentanţii claselor de echivalenţă în anumite puncte din spaţiul euclidian.

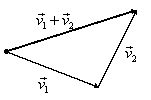Figura I.22.

2º. Prin aplicarea repetată a regulii triunghiului, graţie proprietăţii de asociativitate a adunării vectorilor liberi, în situaţia adunării unui număr arbitrar de vectori se foloseşte regula poligonului ilustrată în figura I.23. În această figură am folosit reprezentarea grafică abuzivă semnalată mai sus. „Poligonul” reprezentat în figura I.23 nu este neapărat o figură plană.

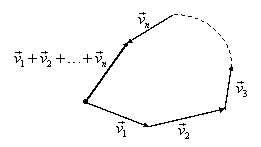Figura I.23.

3º. Regula triunghiului pune în evidenţă următoarea proprietate a surjecţiei canonice (I.92):

(I.A.103)

2.2.2. Înmulţirea vectorilor liberi cu scalari reali

Se defineşte operaţia notată „”, ce asociază oricărei perechi formată dintr-un număr real şi un vector liber un vector liber, prin relaţia:

(I.A.104)

Operaţia (I.A.104) se defineşte prin intermediul unui reprezentant într-un punct al vectorului liber . Rezultatul însă nu depinde de alegerea punctului , deci de reprezentantul vectorului liber.

Astfel, fie punctul diferit de punctul O şi fie şi reprezentanţii vectorului liber în , respectiv . În acest caz avem:

(I.A.105)

Folosind definiţia înmulţirii vectorilor legaţi cu scalari reali şi definiţia relaţiei de echipolenţă, din relaţia (I.A.105) rezultă:

(I.A.106)

Figura I.24 ilustrează cazul în care .

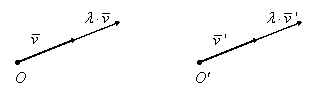Figura I.24.

Relaţia (I.A.106) arată că vectorii legaţi şi aparţin aceleiaşi clase de echivalenţă în raport cu relaţia de echipolenţă pentru orice valoare a scalarului , deci:

(I.A.107)

Relaţia (I.A.107) demonstrează că înmulţirea vectorilor liberi cu scalari reali, definită prin relaţia (I.A.104), nu depinde de reprezentanţii aleşi (nu depinde de alegerea punctului O).

Proprietăţile (i1)-(i4) ale operaţiei de înmulţire a vectorilor legaţi cu scalari reali se transcriu în cazul înmulţirii vectorilor liberi cu scalari reali sub forma:

(I1) ;

(I2) ;

(I3) ;

(I4) .

Observaţii:

1º. Pentru comoditatea scrieri, înmulţirea unui vector liber cu un scalar real se poate scrie în forma , renunţând la punctul aşezat între scalar şi vector, operaţia desemnându-se prin concatenarea celor două simboluri şi .

2º. Din definiţia (I.A.104) sau aplicând proprietăţile (I1)-(I4) se demonstrează relaţiile:

	(I.A.108)
	(I.A.109)
	(I.A.110)

Relaţia (I.A.110) permite utilizarea notaţiei . Astfel se defineşte scăderea (diferenţa) a doi vectori liberi din prin relaţia:

(I.A.111)

Desenată cu ajutorul reprezentanţilor vectorilor liberi , şi , utilizând regula triunghiului, avem situaţia prezentată în figura I.25.

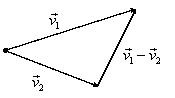Figura I.25.

Astfel, în paralelogramul construit cu reprezentanţii a doi vectori liberi reprezentaţi în acelaşi punct avem situaţia din figura I.26.

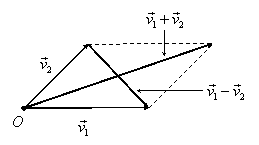Figura I.26.

Diagonala paralelogramului ce pleacă din O este un reprezentant pentru vectorul liber ; cealaltă diagonală (privită ca segment orientat – figura I.26) este un reprezentant al vectorului liber .

3º. Modulul unui vector liber , notat , se defineşte ca fiind valoarea comună a modulului segmentelor orientate echipolente ce aparţin clasei de echivalenţă notată .

Dat fiind scalarul şi vectorul liber nenul , vectorul liber are modulul egal cu , direcţia aceeaşi cu a vectorului liber , iar sensul acelaşi cu sensul lui dacă sau opus sensului lui dacă .

Cu proprietăţile (A1)-(A4) şi (I1)-(I4) avem că mulţimea vectorilor liberi împreună cu cele două operaţii: adunarea vectorilor liberi şi înmulţirea acestora cu scalari reali, formează un -spaţiu liniar.

Aplicaţia (I.A.96):

are proprietăţile:

(i) este bijectivă;

(ii) ;

(iii) .

Se mai spune că este o bijecţie care păstrează operaţiile de spaţiu liniar. Proprietăţile 2 şi 3 de mai sus sunt echivalente cu:

(iv)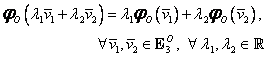

numită şi proprietate de -liniaritate.

O aplicaţie între două spaţii liniare cu proprietăţile (i) şi (iv) de mai sus se numeşte izomorfism de spaţii liniare (vectoriale). În aceste condiţii, vom spune că spaţiile liniare şi sunt izomorfe.

Calitatea de izomorfism generează proprietăţile:

	(I.A.112)
	(I.A.113)

Aplicaţia (I.A.97):

este de asemenea un izomorfism de spaţii liniare, deoarece:

(a) este bijectivă;

(b) .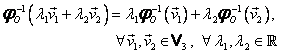

Au loc de asemenea relaţiile:

	(I.A.114)
	(I.A.115)

2.2.3. Baze în spaţiul liniar al vectorilor liberi

Pentru spaţiul liniar al vectorilor liberi se poate demonstra următoarea teoremă:

Teorema 12:

-spaţiul liniar al vectorilor liberi este finit dimensional şi .

Demonstraţie:

Fie un punct fixat arbitrar şi o bază în spaţiul liniar . Vectorii , legaţi în O, sunt necoplanari. Considerăm vectorii liberi:

(I.A.116)

Vom demonstra că este o bază în spaţiul liniar . Pentru aceasta vom arăta că vectorii liberi , sunt liniar independenţi şi formează un sistem de generatori pentru .

Fie scalarii , astfel încât:

(I.A.117)

Cu relaţiile (I.A.112) şi (I.A.116), relaţia (I.A.117) devine:

(I.A.118)

relaţie echivalentă, conform proprietăţii (iv) a izomorfismului , cu relaţia:

(I.A.119)

Cum aplicaţia este injectivă, din (I.A.119) rezultă:

(I.A.120)

ţinând cont de liniar independenţa vectorilor legaţi , din (I.A.120) urmează:

(I.A.121)

Deci, relaţia (I.A.117) implică (I.A.121). Rezultă că vectorii liberi , sunt liniar independenţi.

Demonstrăm în continuare că vectorii liberi , generează spaţiul liniar . Fie un vector liber arbitrar şi reprezentantul vectorului liber în . Deoarece este bază în , rezultă că există trei scalari , , astfel încât:

(I.A.122)

echivalentă cu:

(I.A.123)

Cum aplicaţia este -liniară, din (I.A.123) rezultă:

(I.A.124)

În baza injectivităţii aplicaţiei , relaţia (I.A.124) implică:

(I.A.125)

Am demonstrat astfel că pentru orice vector liber există trei scalari , , astfel încât este satisfăcută relaţia (I.A.125), deci vectorii liberi , formează un sistem de generatori pentru spaţiul liniar .

Concluzia este că reprezintă o bază în spaţiul liniar . Cum mulţimea B este formată din trei elemente, rezultă că dimensiunea spaţiului liniar peste corpul numerelor reale este 3:

(I.A.126)

♦

Observaţii:

1º. Se demonstrează, ca şi în cazul vectorilor legaţi din , că scrierea (I.A.125) este unică. Numerele reale , , din relaţia (I.A.125) se numesc componentele vectorului în baza .

Notând componentele vectorului liber în baza B cu indici superiori şi utilizând convenţia de sumare a indicilor muţi (introdusă în paragraful 1.2.4) descompunerea unică (I.A.125) a vectorului liber în baza considerată devine:

(I.A.127)

Atunci când nu se specifică contrariul, indicii care se repetă iau toate valorile din mulţimea .

2º. Baza din se numeşte ortogonală (respectiv ortonormată) dacă baza corespunzătoare din spaţiul liniar , cu , , este ortogonală (respectiv ortonormată).

2.2.4. Subspaţii liniare remarcabile ale lui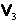

Definiţia 7:

O submulţime proprie se numeşte este subspaţiu liniar al lui dacă sunt îndeplinite condiţiile:

	(I.A.128)
	(I.A.129)

Folosind definiţia de mai sus se demonstrează fără dificultate:

Teorema 13:

este subspaţiu liniar al lui dacă şi numai dacă:

(I.A.130)

Din teorema precedentă rezultă în mod necesar . Mai mult, este un subspaţiu liniar al lui . Subspaţiile liniare ale lui diferite de şi se numesc subspaţii liniare proprii.