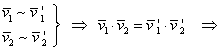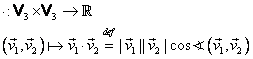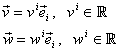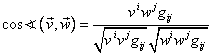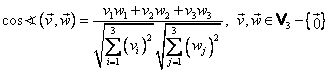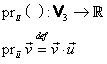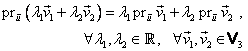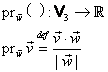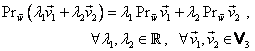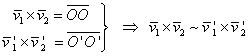2.2.4.1. Dreapta vectorială în

            Fie  o dreaptă în spaţiul euclidian tridimensional.

 

            Definiţia 8:

            Vom numi dreaptă vectorială, notată , o submulţime a lui  definită prin:

(I.A.131)

 

            Conform definiţiei 7 sau teoremei 13 rezultă că  este un subspaţiu liniar propriu al lui . Acesta conţine toţi vectorii liberi cu aceeaşi direcţie dată de dreapta .

 

            Prin analogie cu cazul dreptelor vectoriale din  se demonstrează:

(I.A.132)

            O bază în  este dată de orice vector nenul din . Astfel, dacă , atunci  este bază în . Avem:

astfel încât

(I.A.133)

 

Observaţie:

            1º. Doi vectori liberi  şi  se numesc paraleli (sau coliniari) dacă aparţin aceleiaşi drepte vectoriale. Paralelismul vectorilor  şi  se notează prin .

În particular, vectorul liber nul  este paralel cu oricare alt vector liber din , întrucât  aparţine oricărei drepte vectoriale.

            Dacă cel puţin unul din vectori este nenul (de exemplu ) avem:

astfel încât

(I.A.134)

            Dacă scalarul  din relaţia (I.A.134) este strict pozitiv (respectiv strict negativ) vom spune că vectorii liberi  şi  sunt paraleli şi de acelaşi sens (respectiv de sensuri opuse) şi vom scrie  (respectiv ).

 

2.2.4.2. Planul vectorial în

            Fie  un plan în spaţiul euclidian tridimensional.

 

            Definiţia 9:

            Vom numi plan vectorial, notat , o submulţime a lui  definită prin:

(I.A.135)

 

            Conform definiţiei 9 sau aplicând teorema 13 rezultă că  este un subspaţiu liniar propriu al lui .  conţine toţi vectorii liberi din  ai căror reprezentanţi au dreptele suport paralele cu planul .

 

            La fel ca şi în cazul planului vectorial din  se demonstrează:

(I.A.136)

            O bază în  este dată de oricare doi vectori din  care nu aparţin aceleiaşi drepte vectoriale (care nu sunt paraleli).

            Astfel, dacă  şi , atunci  este o bază în planul vectorial .

            Are loc echivalenţa:

astfel încât

(I.A.137)

            În plus, odată fixaţi vectorii , , descompunerea (I.A.137) este unică.

 

Observaţii:

            1º. Fie  şi  două drepte neparalele, paralele cu planul . Considerăm dreptele vectoriale  şi , şi planul vectorial . ţinând cont de relaţia (I.A.131) rezultă că oricare ar fi un vector liber , există doi vectori,  şi , astfel încât:

(I.A.138)

            Vectorii  şi  din relaţia (I.A.138) sunt unic determinaţi. În acest caz se spune că planul vectorial  este suma directă a dreptelor vectoriale  şi ,  şi se scrie:

;

(I.A.139)

 

            2º. Fie , , trei drepte neparalele în spaţiul euclidian tridimensional. Considerăm dreptele vectoriale , , corespunzătoare. În conformitate cu relaţia (I.A.125), oricare ar fi un vector liber , există trei vectori, , , astfel încât:

(I.A.140)

            În plus, vectorii , , din relaţia (I.A.140) sunt unic determinaţi. Vom spune că spaţiul liniar  este suma directă a dreptelor vectoriale , , ceea ce se scrie:

;

(I.A.141)

 

            3º. Fie  un plan şi  o dreaptă neparalelă cu planul . Analog se demonstrează că:

;

(I.A.142)

 

2.3. Operaţii cu vectori liberi

2.3.1. Produsul scalar al vectorilor liberi

            Este o operaţie, notată cu „”, care asociază oricărei perechi de vectori liberi un număr real:

(I.A.143)

 

            Definiţia (I.A.143) nu depinde de alegerea polului , deci nu depinde de reprezentanţii vectorilor liberi  şi .

 

            Într-adevăr, fie , şi , reprezentanţii celor doi vectori liberi în punctele distincte O şi  (figura I.27).

 

 

 

 

 

 

 

 

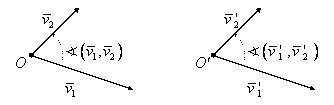Figura I.27.

 

            Are loc implicaţia:

,	(I.A.144)

deoarece din , , rezultă , . De asemenea,  ca unghiuri cu laturile respectiv paralele.

 

Observaţie:

            1º. Modulul unui vector liber , notat cu , a fost definit ca fiind valoarea comună a modulului segmentelor orientate echipolente ce aparţin clasei de echivalenţă notată .

            De asemenea, putem defini unghiul a doi vectori liberi  şi , notat , ca valoarea unghiului format de doi reprezentanţi ai acestor vectori în  (am observat, mai sus, că acest unghi nu depinde de alegerea punctului O).

            Cu aceste notaţii, definiţia (I.A.143) a produsului scalar a doi vectori liberi se poate da şi sub forma:

(I.A.145)

 

            Proprietăţile produsului scalar a doi vectori liberi le reproduc pe cele ale produsului scalar a doi vectori legaţi din :

(S1)     ;

(S2)     ;

(S3)     ;

(S4)     .

            În scrierea proprietăţii (S4) am utilizat notaţia .

 

            Fie  o bază în  şi  doi vectori arbitrari ale căror descompuneri în baza B se scriu, utilizând convenţia indicilor muţi, sub forma:

(I.A.146)

            Notând:

(I.A.147)

cu proprietăţile (S1)-(S3) rezultă expresia produsului scalar :

(I.A.148)

 

            În particular, pentru , ţinând cont că din definiţia (I.A.145) se obţine:

(I.A.149)

rezultă modulul vectorului  sub forma:

(I.A.150)

            De asemenea, din definiţia (I.A.145) şi relaţiile (I.A.148) şi (I.A.150), dacă vectorii  şi  sunt nenuli, , atunci unghiul format de cei doi vectori este dat de:

(I.A.151)

 

            Doi vectori liberi  se numesc ortogonali şi notăm aceasta prin  dacă reprezentanţii lor într-un punct oarecare O din spaţiu sunt ortogonali. ţinând cont de convenţia că vectorul legat nul, , este ortogonal pe orice vector din , se obţine că vectorul liber nul, , este ortogonal pe orice vector din .

            Aplicând teorema 8, rezultă următoarea echivalenţă:

(I.A.152)

            De asemenea, se observă că: dacă produsul scalar a doi vectori liberi nenuli este zero, atunci direcţiile celor doi vectori liberi sunt perpendiculare.

 

Observaţii:

            1º. Aşa cum am mai precizat, baza  din  este ortonormată dacă baza corespunzătoare  din spaţiul liniar , cu , , este ortonormată. Din definiţia (I.A.37) şi relaţiile (I.A.50), rezultă că pentru o bază ortonormată sunt satisfăcute relaţiile:

(I.A.153)

unde  notează simbolul lui Kronecker definit prin relaţia (I.A.51):

            În cazul unei baze ortonormate indicii componentelor vectorilor din relaţiile (I.A.146) se scriu jos:

(I.A.154)

astfel că relaţiile (I.A.148), (I.A.150) şi (I.A.151) devin:

	(I.A.155)
	(I.A.156)
	(I.A.157)

 

            2º. Fie  un versor liber, . Numim proiecţia vectorului arbitrar  pe versorul  aplicaţia:

(I.A.158)

            Pe baza proprietăţilor produsului scalar se demonstrează că aplicaţia (I.A.158) este -liniară:

(I.A.159)

            De asemenea se observă că au loc echivalenţele:

(I.A.160)

            Dacă  arbitrar, atunci  este un versor liber, . Definim proiecţia vectorului  pe vectorul  aplicaţia:

(I.A.161)

            Evident, proprietăţile (I.A.159) şi (I.A.160) se păstrează şi pentru aplicaţia (I.A.161).

 

            3º. Definim proiecţia vectorială a vectorului  pe vectorul  fixat aplicaţia:

(I.A.162)

            Pentru  fixat, avem în definitiv:

,

(I.A.163)

de unde rezultă că şi aplicaţia (I.A.162) este -liniară:

(I.A.164)

 

2.3.2. Produsul vectorial al vectorilor liberi

            Este o operaţie, notată cu „”, care asociază oricărei perechi de vectori liberi un vector liber:

(I.A.165)

            Definiţia (I.A.165) a operaţiei produs vectorial nu depinde de alegerea polului , deci nu depinde de reprezentanţii vectorilor liberi  şi .

            Într-adevăr, fie , şi , reprezentanţii celor doi vectori liberi în punctele distincte O şi .

            Dacă vectorii  şi  legaţi în O sunt coliniari atunci şi vectorii  şi  legaţi în O sunt coliniari. Din definiţia produsului vectorial al vectorilor legaţi se obţine:

(I.A.166)

 

            Dacă vectorii  şi  sunt necoliniari atunci nici vectorii  şi  nu sunt coliniari (figura I.28).

 

 

 

 

 

 

 

 

 

 

 

 

Figura I.28.

 

 În acest caz  ca unghiuri cu laturile respectiv paralele. Planele π şi π' determinate de  şi , respectiv  şi , sunt paralele. Prin urmare şi în acest caz are loc implicaţia:

 

 

---