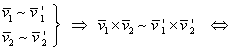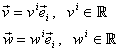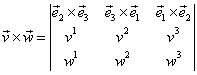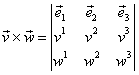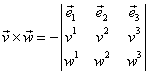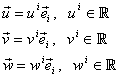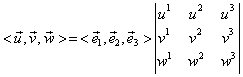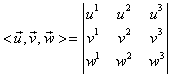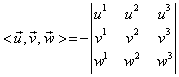,

(I.A.167)

            Relaţia (I.A.167) arată că produsul vectorial a doi vectori liberi nu depinde de reprezentanţi.

 

            Pornind de la definiţie, se pot demonstra următoarele proprietăţi ale produsului vectorial a doi vectori liberi:

(V1)     ;

(V2)     ;

(V3)     .

 

            Din proprietăţile de mai sus rezultă că operaţia definită prin relaţia (I.A.159) este -liniară în ambele argumente şi anticomutativă (proprietatea V1).

 

            Fie  o bază în  şi  doi vectori arbitrari ale căror descompuneri în baza B sunt date de (I.A.146):

(I.A.168)

            Prin analogie cu cazul vectorilor legaţi din  se arată că produsul vectorial  se poate scrie sub forma determinantului simbolic:

(I.A.169)

 

            În cazul în care baza  este ortonormată dreaptă:

(I.A.170)

relaţia (I.A.169) devine:

(I.A.171)

            Dacă baza  este ortonormată stângă:

(I.A.172)

relaţia (I.A.169) devine:

(I.A.173)

 

            Fie acum . Condiţia ca un vector liber  să aparţină dreptei vectoriale  este ca . Cu ajutorul operaţiei produs vectorial această condiţie se poate scrie sub forma:

 

            Teorema 14:

            Are loc echivalenţa:

(I.A.174)

 

            În enunţul teoremei 14 am folosit convenţia că vectorul liber nul  este paralel (coliniar) cu orice vector liber.

 

 

2.3.3. Produsul mixt al vectorilor liberi

            Produsul mixt al vectorilor liberi din , notat „”, este o aplicaţie care asociază, în mod univoc, oricărui triplet de vectori liberi un număr real:

(I.A.175)

            Produsul mixt a trei vectori liberi se defineşte prin intermediul operaţiilor de produs scalar şi produs vectorial definite anterior.

 

            Proprietăţile acestei aplicaţii se transcriu în mod asemănător proprietăţilor produsului mixt a trei vectori legaţi din :

(M1)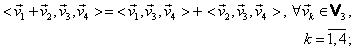   

(M2)   

unde 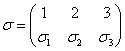 este o permutare a mulţimii , iar  notează signatura permutării ;

(M3)    .

            Din proprietăţile (M1)-(M3) rezultă că produsul mixt este o operaţie -liniară şi comutativă ciclic în raport cu oricare din cele trei argumente.

            Fie  o bază în  şi  trei vectori arbitrari ale căror descompuneri în baza B sunt:

(I.A.176)

            La fel ca în cazul vectorilor legaţi se demonstrează relaţia:

(I.A.177)

 

            În cazul în care baza  este ortonormată dreaptă:

(I.A.178)

relaţia (I.A.177) devine:

(I.A.179)

            Dacă baza  este ortonormată stângă:

(I.A.180)

relaţia (I.A.177) devine:

(I.A.181)

 

Observaţii:

            1º. Dacă baza  din spaţiul liniar  are proprietatea , baza B se numeşte bază orientată drept (sau bază dreaptă). Dacă  baza B se numeşte bază orientată stâng (sau bază stângă).

            2º. Fie  doi vectori liberi din spaţiul liniar  neparaleli, . Aşa cum am mai demonstrat anterior ei determină, în mod unic, un plan vectorial notat :

(I.A.182)

            Proprietatea de apartenenţă la acest plan vectorial se poate scrie cu ajutorul produsului mixt. Astfel, dacă , , atunci are loc echivalenţa:

(I.A.183)

 

            3º. Cu ajutorul produsului mixt al vectorilor liberi se poate caracteriza liniar independenţa sau liniar dependenţa a trei vectori liberi din spaţiul liniar . Astfel, au loc echivalenţele:

- liniar dependenţi     - liniar independenţi

(I.A.184)

 

            Pe baza observaţiilor anterioare se poate demonstra teorema de caracterizare a bazelor din spaţiul liniar :

 

            Teorema 15:

            Fie  trei vectori liberi din . Are loc echivalenţa:

bază în

(I.A.185)

 

3.Spaţii afine

            Construcţia matematică anterioară (definirea mulţimii vectorilor liberi  drept mulţimea claselor de echivalenţă ale relaţiei de echipolenţă definită pe mulţimea segmentelor orientate) sugerează definirea unui obiect matematic mai elaborat, numit spaţiu afin.

 

            Definiţia 10:

            Fie  o mulţime ale cărei elemente le numim puncte,  un -spaţiu liniar şi  o funcţie ce asociază în mod univoc fiecărei perechi ordonată de puncte din  un element din . Tripletul  se numeşte spaţiu afin dacă sunt îndeplinite condiţiile:

(SA1)             

(SA2)              astfel încât:

 

Consecinţe:

            Din (SA1) rezultă pentru :

(I.A.186)

unde am notat cu e vectorul nul (elementul neutru la adunare) din spaţiul liniar .

 

            Pentru , din (SA1) şi relaţia (I.A.180) se obţine:

(I.A.187)

 

 

 

Observaţii:

            1º. Elementele din definiţia 10 capătă denumiri specifice. Astfel:

-          se numeşte spaţiu suport, iar elementele sale punctele spaţiului afin;

-          se numeşte spaţiu director, iar elementele sale vectori directori;

-          se numeşte funcţia de structură a spaţiului afin.

 

            2º. Dacă -spaţiul liniar este finit dimensional şi , , atunci spaţiul afin  se numeşte finit dimensional, având dimensiunea .

            Tripletul  unde  este spaţiul euclidian tridimensional,  spaţiul liniar real al vectorilor liberi şi  surjecţia canonică definită prin relaţia (I.A.92) este un exemplu tipic de spaţiu afin. Condiţiile (SA1) şi (SA2) sunt satisfăcute în conformitate cu (I.A.103) respectiv (I.A.95). Acest spaţiu afin este finit dimensional (de dimensiune 3) şi constituie suportul intuitiv pentru spaţii afine mai generale.

 

            Deşi de multe ori nu se precizează în mod explicit, în modelarea matematică a fenomenelor mecanicii clasice se folosesc copios proprietăţi ale spaţiului afin . Exemplificăm aceasta prin noţiunea de reper afin în .

 

            Definiţia 11:

            Fie  o bază în spaţiul liniar  şi  un punct fixat. Ansamblul  se numeşte reper afin în .

 

            Punctul fixat  poartă numele de origine a reperului afin . Vectorul liber  se numeşte vectorul de poziţie al punctului A în raport cu reperul . Întrucât are loc scrierea unică:

(I.A.188)

numerele reale , poartă numele de coordonate carteziene ale punctului A în raport cu reperul afin .

            Odată fixat un reper afin , relaţia (I.A.188) şi proprietăţile spaţiului afin  stabilesc o corespondenţă biunivocă între punctele din spaţiul euclidian tridimensional  şi tripletele ordonate de numere reale .

            Vectorul de poziţie (I.A.188) şi baza  se desenează de obicei prin reprezentanţii lor în originea reperului afin , utilizând abuzul semnalat anterior.

 

 

 

 

 

 

 

 

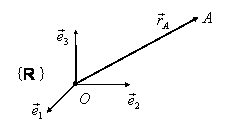Figura I.29.

 

            Faptul că punctul  are coordonatele carteziene , în raport cu reperul  se scrie în forma .

 

            În mod similar se introduc repere afine în spaţii afine n‑dimensionale, , .

 

---