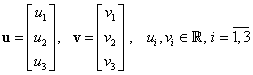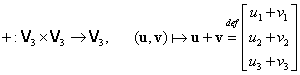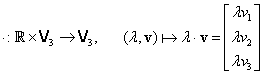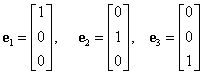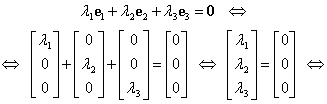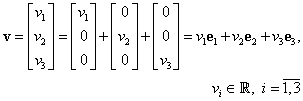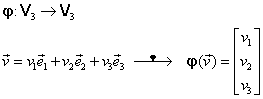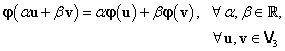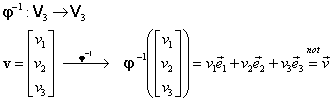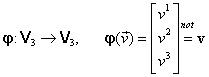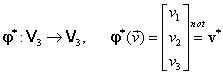Capitolul III

REPREZENTăRI SIMBOLICE MATRICEALE

 

A. Breviar teoretic

 

1. Mulţimea matricelor coloană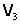

            Fie  mulţimea matricelor coloană cu trei elemente numere reale. Vom nota în cele ce urmează cu litere latine mici bold elementele din  (de exemplu ). Două elemente generice din  sunt de forma:

(III.A.1)

 

1.1. Spaţiul liniar real al matricelor coloană

            Cu ajutorul a două operaţii definite mai jos mulţimea matricelor coloană poate fi organizată ca -spaţiu liniar.

 

            Definim adunarea matricelor coloană prin:

(III.A.2)

unde elementele  sunt de forma (III.A.1), şi operaţia de înmulţire a elementelor din  cu scalari reali prin:

(III.A.3)

 

            Operaţia definită prin relaţia (III.A.2) are proprietăţile:

(AC1) 

(AC2) 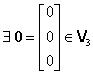 astfel încât: ;

(AC3)  astfel încât ;

            dacă 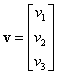, atunci ;

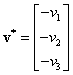(AC4)  .

            Demonstraţiile proprietăţilor (AC1)-(AC4) sunt imediate folosind definiţia şi proprietăţile operaţiilor definite pe corpul numerelor reale. Rezultă că  este grup abelian.

 

            Operaţia definită prin relaţia (III.A.3) are proprietăţile:

(IC1)   ;

(IC2)   ;

(IC3)   ;

(IC4)   .

            Demonstraţia proprietăţilor (IC1)-(IC4) este banală, folosind definiţia şi proprietăţile corpului numerelor reale .

            Sunt valabile identităţile:

	(III.A.4)
	(III.A.5)
	(III.A.6)

            Proprietatea (III.A.4) justifică notaţia .

            ţinând cont de proprietăţile (AC1)-(AC4) şi (IC1)-(IC4), mulţimea matricelor coloană  este organizată ca spaţiu liniar real.

 

            Teorema 1:

            Spaţiul liniar  este finit peste corpul numerelor reale şi .

 

            Demonstraţie:

            Fie elementele din  notate , date de:

(III.A.7)

            Demonstrăm mai întâi că elementele  sunt liniar independente. Fie

	(III.A.8)

            Mulţimea  este sistem de generatori pentru . Fie un element  arbitrar. Avem:

(III.A.9)

            Prin urmare tripletul  este bază în spaţiul liniar real , deci .    ♦

1.2. Izomorfismul dintre 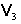 şi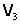

            Fie  spaţiul liniar real al vectorilor liberi din spaţiul euclidian tridimensional şi  o bază ortonormată în . Un element generic din  este de forma:

(III.A.10)

 

            Definim aplicaţia:

(III.A.11)

            Cu notaţia (III.A.1) legea de corespondenţă a aplicaţiei (III.A.11) se scrie:

(III.A.12)

 

            Se poate demonstra

 

            Teorema 2:

            Aplicaţia (III.A.11) este izomorfism de spaţii liniare.

 

            Demonstraţie:

            Se verifică cu uşurinţă că aplicaţia  (III.A.11) este bijectivă şi are proprietatea:

(III.A.13)

♦

 

Observaţii:

            1º. Aplicaţia inversă aplicaţiei (III.A.11):

(III.A.14)

este de asemenea izomorfism de spaţii liniare.

 

            2º. Prin intermediul aplicaţiei (III.A.11) au loc corespondenţele:

(III.A.15)

 

            3º. Dacă baza  fixată în spaţiul liniar  nu este ortonormată, notând cu  reciproca bazei , un vector arbitrar  se poate scrie în una din formele:

	(III.A.16)
	(III.A.17)

            În acest caz se pot defini două izomorfisme de spaţii liniare din  în :

	(III.A.18)
	(III.A.19)

            Aplicaţia  (III.A.18) asociază unui vector arbitrar din  descompus în baza , matricea coloană a componentelor sale contravariante, iar aplicaţia  (III.A.19) asociază unui vector arbitrar din  descompus în baza , matricea coloană a componentelor sale covariante. Aceste izomorfisme fac obiectul problemei III.1. Dacă baza  este ortonormată, izomorfismele  şi  coincid.

---