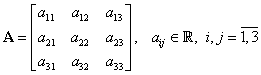
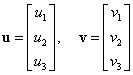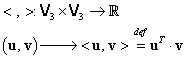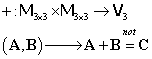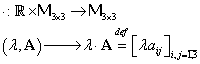1.3. Produsul scalar în

            Fie  o bază ortonormată în  şi , respectiv , doi vectori liberi arbitrari:

	(III.A.20)
	(III.A.21)

            După cum am arătat în paragraful I.2.3.1, în această ipoteză avem:

,	(III.A.22)

            Cu notaţiile  şi :

 

(III.A.23)

relaţia (III.A.22) poate fi scrisă sub forma:

,	(III.A.24)

unde  notează matricea linie, transpusă matricei coloană u.

            Observaţia (III.A.24) permite definirea pe  a operaţiei produs scalar, notată „”, prin relaţia:

(III.A.25)

            Se constată, fără dificultate, că aplicaţia (III.A.25) are proprietăţile:

(S1)     ;

(S2)     ;

(S3)     ;

(S4)     ;   .

 

            Prin urmare, spaţiul liniar real , înzestrat cu produsul scalar dat de relaţia (III.A.25) este un spaţiu liniar (vectorial) prehilbertian.

 

Observaţii:

            1º. Două elemente  se numesc ortogonale dacă  şi vom nota aceasta, ca şi în cazul vectorilor liberi, prin . Aşadar, are loc echivalenţa:

(III.A.26)

            Din relaţia (III.A.26) rezultă că, prin definiţie, elementul  este ortogonal pe orice element din .

            Facem observaţia că în acest caz proprietatea  (ortogonalitatea a două matrice coloană) nu mai păstrează suportul intuitiv din cazul spaţiilor liniare  sau . Dacă baza  fixată în  este ortonormată, atunci are loc echivalenţa:

(III.A.27)

unde  este izomorfismul dat de relaţia (III.A.11).

 

            2º. Întrucât matricele coloană , date de relaţia (III.A.7) verifică identităţile:

(III.A.28)

unde  notează simbolul lui Kronecker, vom spune că baza  din  este ortonormată. ţinând cont de relaţiile (III.A.15), putem trage concluzia că izomorfismul (III.A.11) transformă bazele ortonormate din  în baze ortonormate din .

 

            3º. Cazul izomorfismelor (III.A.18) şi (III.A.19) este studiat în detaliu în problema III.1.

 

            Produsul scalar definit prin relaţia (III.A.25) permite introducerea unei norme (lungimi sau modul) pentru o matrice coloană din . Astfel, definim:

(III.A.29)

            Se demonstrează, folosind proprietăţile produsului scalar dat de relaţia (III.A.25) că aplicaţia (III.A.29) are proprietăţile:

(N1)    ;   ;

(N2)    ;

(N3)    .

            Se mai spune că  este un spaţiu liniar (vectorial) normat în raport cu norma dată prin relaţia (III.A.29), indusă de produsul scalar (III.A.25)).

 

Observaţii:

            1º. Din relaţiile (III.A.24) şi (III.A.25) rezultă:

	(III.A.30)
	(III.A.31)

prin urmare izomorfismul (III.A.11) păstrează produsele scalare definite pe cele două spaţii liniare şi, implicit, „lungimea” vectorilor.

 

            2º. Întrucât inegalitatea:

(III.A.32)

se transcrie, cu notaţiile  şi , în forma:

(III.A.33)

se poate defini „unghiul” a două matrice coloană nenule din  prin:

(III.A.34)

 

            3º. Cazul izomorfismelor (III.A.18) şi (III.A.19) este studiat în detaliu în problema III.1.

2. Mulţimea matricelor pătratice

            Fie  mulţimea matricelor pătratice cu elemente numere reale având trei linii şi trei coloane. Un element generic  este de forma:

(III.A.35)

            Uneori, vom scrie succint matricea  în forma:

(III.A.36)

 

2.1. Spaţiul liniar real al matricelor pătratice

            Mulţimea  poate fi organizată ca spaţiu liniar real.

            Adunarea matricelor din  se defineşte prin:

(III.A.37)

unde matricea C este dată de relaţia:

(III.A.38)

pentru:

	(III.A.39)
	(III.A.40)

 

            Se verifică, fără dificultate, proprietăţile:

(AP1) 

(AP2)  astfel încât: ;

            Matricea  are elementele ;

(AP3)  astfel încât ;

            Dacă , atunci ;

(AP4)  .

            ţinând cont de proprietăţile (AP1)-(AP4) rezultă că  este grup abelian.

 

            Înmulţirea cu scalari reali a matricelor din  se defineşte prin:

(III.A.41)

unde am considerat matricea A de forma .

            Se verifică fără dificultate proprietăţile:

(IP1)    ;

(IP2)    ;

(IP3)    ;

(IP4)    .

şi identităţile:

	(III.A.42)
	(III.A.43)
	(III.A.44)

            Proprietatea (III.A.42) justifică utilizarea notaţiei .

 

 Prin urmare, mulţimea matricelor pătratice  este un spaţiu liniar real în raport cu operaţiile (III.A.37) şi (III.A.41).

---