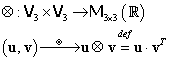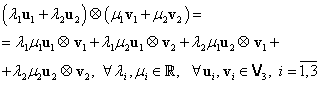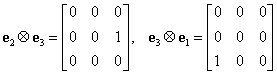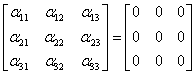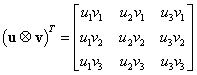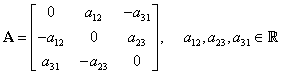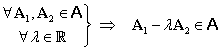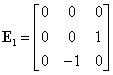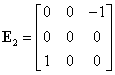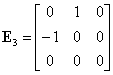2.2. Produsul tensorial al matricelor coloană din

            Fie aplicaţia:

(III.A.45)

numită produs tensorial al matricelor coloană din .

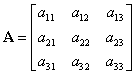
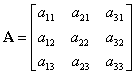
            Dacă , atunci matricea pătratică  are elementele .

            Aplicaţia produs tensorial este -liniară în cele două argumente, după cum rezultă imediat din definiţia (III.A.45):

(III.A.46)

 

            Fie , elementele bazei din  date prin relaţia (III.A.7). Matricea pătratică  are toate elementele egale cu zero cu excepţia celui aflat la intersecţia liniei i cu coloana j, care este egal cu 1. De exemplu:

(III.A.47)

etc.

 

           

 

 

 

 

Putem enunţa acum:

 

            Teorema 3:

            Spaţiul liniar  este finit peste corpul numerelor reale şi .

 

            Demonstraţie:

            Vom demonstra că mulţimea  este o bază în spaţiul liniar real . Pentru a demonstra liniara independenţă a acestor elemente considerăm combinaţia liniară ce are drept rezultat matricea nulă:

(III.A.48)

            În scrierea relaţiei (III.A.48) am folosit convenţia indicilor muţi. Cu observaţia anterioară privind matricele pătratice , relaţia (III.A.48) este echivalentă cu:

(III.A.49)

            Din (III.A.49) rezultă:

(III.A.50)

deci elementele , sunt liniar independente în spaţiul liniar real .

 

            Demonstrăm în continuare că mulţimea  este un sistem de generatori pentru .

            Fie  o matrice pătratică oarecare din . În baza aceleiaşi observaţii privind matricele , şi ţinând cont de definiţia (III.A.41) avem:

(III.A.51)

folosind convenţia indicilor muţi.

 

            Am arătat astfel că  este o bază în spaţiul liniar real . Faptul că baza  are 9 elemente, probează enunţul teoremei.    ♦

 

2.3. Subspaţii liniare remarcabile ale lui

            În continuare, vom pune în evidenţă două subspaţii liniare remarcabile ale spaţiului liniar real al matricelor pătratice de numere reale cu trei linii şi trei coloane .

            Reamintim:

 

            Definiţia 1:

             este subspaţiu liniar al lui  dacă au loc implicaţiile:

	(III.A.52)
	(III.A.53)

 

            Din definiţia de mai sus rezultă fără dificultate:

 

            Teorema 4:

             este subspaţiu liniar al lui  dacă are loc implicaţia:

(III.A.54)

            Definiţia 2:

            Fie matricea arbitrară . Vom numi transpusa matricei A, notată , matricea definită prin , unde .

 

            Are loc următoarea teoremă ce rezultă imediat din definiţia precedentă şi operaţiile ce definesc structura de spaţiu liniar pe :

 

            Teorema 5:

            Operaţia de transpunere a matricelor din  are proprietăţile:

	(III.A.55)
	(III.A.56)

 

Observaţii:

            1º. Dacă matricea  este de forma:

(III.A.57)

transpusa matricei , notată , se obţine schimbând liniile de un anumit rang în locul coloanelor de acelaşi rang din matricea A:

(III.A.58)

            2º. Fie , două elemente arbitrare din . Conform definiţiei (III.A.45) avem:

(III.A.59)

            Se observă că:

(III.A.60)

şi:

(III.A.61)

            Deoarece înmulţirea numerelor reale este comutativă, din relaţiile (III.A.60) şi (III.A.61) rezultă identitatea:

,	(III.A.62)

 

            3º. Cu scrierea (III.A.51) pentru o matrice pătratică arbitrară din  şi relaţia (III.A.62) avem:

	(III.A.63)
	(III.A.64)

unde am utilizat convenţia indicilor muţi.

 

2.3.1. Subspaţiul liniar al matricelor antisimetrice

            Definiţia 3:

            O matrice  se numeşte antisimetrică dacă satisface condiţia:

(III.A.65)

Observaţie:

            1º. Din definiţia transpusei unei matrice rezultă că matricea  este antisimetrică dacă şi numai dacă:

(III.A.66)

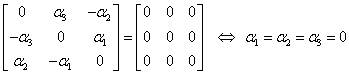
            În particular pentru , din condiţia (III.A.66) rezultă:

(III.A.67)

deci elementele de pe diagonala principală a unei matrice antisimetrice sunt nule.

            Forma generală a unei matrice antisimetrice este:

(III.A.68)

            În particular, matricea pătratică nulă  este antisimetrică.

 

            Fie  mulţimea matricelor antisimetrice din :

(III.A.69)

 

            Teorema 6:

             este subspaţiu liniar de dimensiune trei al lui : .

 

            Demonstraţie:

            Fie :

	(III.A.70)
	(III.A.71)

            ţinând cont de relaţiile (III.A.55) şi (III.A.56), are loc şirul de egalităţi:

	(III.A.72)

adică matricea  este antisimetrică.

            Prin urmare are loc implicaţia:

(III.A.73)

            Conform teoremei 4, rezultă că  este subspaţiu liniar al lui .

 

            Fie matricele antisimetrice:

	(III.A.74)
	(III.A.75)
	(III.A.76)

            Vom demonstra că  este o bază în subspaţiul liniar .

            Pentru a demonstra că matricele , sunt liniar independente considerăm combinaţia liniară:

(III.A.77)

            Cu expresiile (III.A.74)-(III.A.76) ale matricelor , relaţia (III.A.77) este echivalentă cu:

(III.A.78)

deci matricele , sunt elemente liniar independente ale spaţiului liniar .

 

            Matricele , formează un sistem de generatori pentru  deoarece din relaţiile (III.A.68) şi (III.A.74)-(III.A.76) rezultă:

astfel încât:

(III.A.79)

 

            Prin urmare,  este o bază în spaţiul liniar , deci .    ♦

 

Observaţie:

            1º. Din relaţiile (III.A.74)-(III.A.76) cu notaţiile (III.A.7) avem:

	(III.A.80)
	(III.A.81)
	(III.A.82)

---