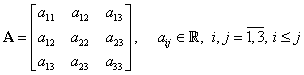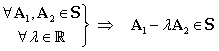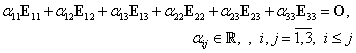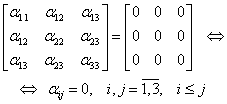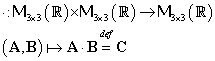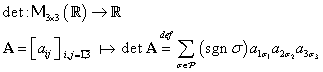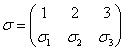2.3.2. Subspaţiul liniar al matricelor simetrice

            Definiţia 4:

            O matrice  se numeşte simetrică dacă: satisface condiţia:

(III.A.83)

 

Observaţie:

            1º. Din definiţia transpusei unei matrice rezultă că matricea  este simetrică dacă şi numai dacă:

(III.A.84)

            Forma generală a unei matrice simetrice este:

(III.A.85)

            În relaţia (III.A.85) se observă simetria elementelor faţă de diagonala principală a matricei .

            În particular, matricea pătratică nulă  este simetrică.

 

            Fie  mulţimea matricelor simetrice din :

(III.A.86)

 

            Teorema 7:

             este subspaţiu liniar de dimensiune şase al lui : .

 

            Demonstraţie:

            Fie :

	(III.A.87)
	(III.A.88)

            ţinând cont de relaţiile (III.A.55) şi (III.A.56), are loc şirul de egalităţi:

	(III.A.89)

adică matricea  este antisimetrică.

            Prin urmare are loc implicaţia:

(III.A.90)

            Conform teoremei 4, rezultă că  este subspaţiu liniar al lui .

 

            Fie matricele simetrice:

(nesumat)	(III.A.91)
	(III.A.92)
	(III.A.93)
	(III.A.94)

            Vom demonstra că  este o bază în subspaţiul liniar .

            Pentru a demonstra că matricele , sunt liniar independente considerăm combinaţia liniară:

(III.A.95)

            Cu expresiile (III.A.91)-(III.A.94) ale matricelor , relaţia (III.A.95) este echivalentă cu:

(III.A.96)

deci matricele , sunt elemente liniar independente ale spaţiului liniar .

 

            Matricele , formează un sistem de generatori pentru  deoarece din relaţiile (III.A.85) şi (III.A.91)-(III.A.94) rezultă:

astfel încât:

(III.A.97)

            Prin urmare,  este o bază în spaţiul liniar , deci .    ♦

            Cu privire la cele două subspaţii liniare  şi  ale spaţiului liniar real  se poate enunţa următoarea teoremă:

 

            Teorema 8:

            Spaţiul liniar real al matricelor pătratice  este suma directă a subspaţiilor liniare  şi :

(III.A.98)

            Demonstraţie:

            Vom demonstra mai întâi că orice matrice pătratică  se scrie ca suma dintre o matrice antisimetrică şi o matrice simetrică. Într-adevăr, avem:

(III.A.99)

unde:

	(III.A.100)
	(III.A.101)

            Din (III.A.100) rezultă:

(III.A.102)

iar din (III.A.101) avem:

(III.A.103)

 

            Unicitatea scrierii matricei  ca suma dintre o matrice antisimetrică şi o matrice simetrică se demonstrează presupunând că există  şi  astfel încât:

(III.A.104)

            Din relaţia (III.A.104), prin transpunere, rezultă:

(III.A.105)

            Din (III.A.104) şi (III.A.105) se obţine:

	(III.A.106)
	(III.A.107)

            Cum , teorema este demonstrată.    ♦

 

2.4. Monoidul

            Definim operaţia de înmulţire a matricelor pătratice din , notată „”, prin:

(III.A.108)

unde elementele matricei  sunt date de:

(III.A.109)

            În relaţia (III.A.109) am notat ,  şi am folosit regula de sumare a indicilor muţi.

            Folosind definiţia anterioară şi proprietăţile corpului numerelor reale se demonstrează următoarele proprietăţi:

(M1)    ;

(M2)    astfel încât:

matricea I este: , unde  este simbolul lui Kronecker.

 

            Cu proprietăţile (M1) – (M2) are loc:

 

            Teorema 9:

             este monoid în raport cu operaţia de înmulţire a matricelor pătratice.

 

            Un element A al monoidului  se numeşte inversabil dacă are loc:

(M3)    astfel încât .

            În continuare, vom stabili în ce condiţii o matrice pătratică  este inversabilă.

 

            Definim aplicaţia notată „det” prin:

(III.A.110)

unde:

(III.A.111)

reprezintă o permutare a mulţimii ,  este signatura pemutării  iar  este mulţimea celor  permutări de forma (III.A.111).

            Folosind definiţia (III.A.110) se demonstrează proprietăţile:

	(III.A.112)
	(III.A.113)
	(III.A.114)

            Cu definiţia (III.A.108) se demonstrează de asemenea:

(III.A.115)

---