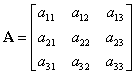
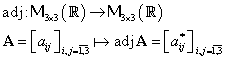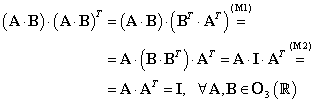Teorema 10:

            Un element  este inversabil dacă şi numai dacă .

            Demonstraţie:

            Fie  o matrice pătratică din :

(III.A.116)

            Definim aplicaţia unară notată „adj”:

(III.A.117)

unde elementele , sunt date de:

, ,

, ,

, ,

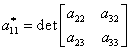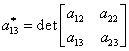
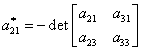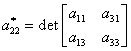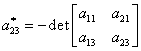
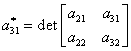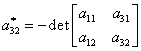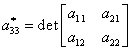
(III.A.118)

            Se demonstrează fără dificultate relaţiile:

,	(III.A.119)
,	(III.A.120)

            Pentru simplificarea scrierii vom nota:

,	(III.A.121)

            Relaţiile (III.A.119) – (III.A.120) se scriu în forma matriceală:

(III.A.122)

            Prin urmare, în ipoteza  matricea A este inversabilă şi:

(III.A.123)

            Teorema este astfel demonstrată.    ♦

 

Observaţie:

            1º. Pentru determinarea adjunctei matricei , notată , se procedează astfel:

-         se determină transpusa matricei , notată ;

-         matricea adjunctă  se obţine înlocuind fiecare element al matricei  cu complementul său algebric. Complementul algebric al elementului , se determină calculând determinantul matricei pătratice de ordinul 2 obţinută prin „tăierea” liniei i şi coloanei j din , şi înmulţindu-l apoi cu .

 

            2º. Operaţia unară definită prin relaţia (III.A.117) are proprietăţile:

	(III.A.124)
	(III.A.125)
	(III.A.126)
	(III.A.127)

care se demonstrează cu uşurinţă folosind definiţiile.

 

 

2.5. Grupul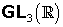

            Vom nota prin  mulţimea elementelor inversabile din monoidul :

(III.A.128)

            Matricele din  le vom numi nesingulare. Matricele din  se vor numi matrice singulare. Cu proprietăţile (M1) – (M3) şi teorema 10 avem:

 

            Teorema 11:

             este grup necomutativ în raport cu înmulţirea matricelor.

 

Observaţie:

            1º. Folosind relaţiile (III.A.123) – (III.A.125) se obţine:

	(III.A.129)
	(III.A.130)

 

2.5.1. Subgrupul matricelor ortogonale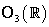

            Definiţie:

            O submulţime strictă  se numeşte subgrup al grupului  dacă are loc implicaţia:

(III.A.131)

 

            Definiţie:

            O matrice  se numeşte ortogonală dacă:

(III.A.132)

 

            Considerăm mulţimea matricelor ortogonale din :

(III.A.133)

 

            Teorema 12:

             este subgrup al grupului .

 

            Demonstraţie:

            Din condiţia de ortogonalitate a matricei :

(III.A.134)

şi relaţiile (III.A.112), (III.A.114) avem:

(III.A.135)

prin urmare:

(III.A.136)

            Din relaţia (III.A.136) rezultă că , deci .

            Fie :

		(III.A.137)
	(III.A.138)

            Prin calcule succesive obţinem:

(III.A.139)

            Relaţia (III.A.139) arată că are loc implicaţia:

(III.A.140)

            Deci  este subgrup al grupului  numit subgrupul (grupul) matricelor ortogonale din .    ♦

 

2.5.2. Subgrupul matricelor ortogonale proprii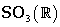

            Vom numi mulţimea matricelor ortogonale proprii, notată , mulţimea:

(III.A.141)

            Evident are loc incluziunea strictă .

 

            Teorema 13:

             este subgrup al grupului .

 

            Demonstraţie:

            Fie :

	(III.A.142)
	(III.A.143)

            Cu observaţia , rămâne de calculat :

(III.A.144)

            Prin urmare:

(III.A.145)

 Teorema este astfel demonstrată. ♦

---