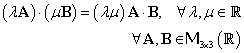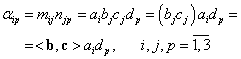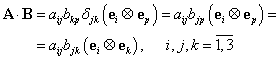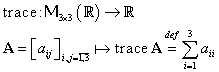Observaţie:

            1º. Elementele grupului  modelează rotaţiile corpurilor rigide în spaţiul euclidian tridimensional. De aceea matricele din  se mai numesc matrice de rotaţie.

 

            2º. Din (III.A.141) condiţiile , arată că matricea  depinde de cel mult trei parametri scalari independenţi:

(III.A.146)

            Operaţia de alegere a acestor parametri poartă numele de parametrizare a grupului . Există mai multe parametrizări folosite în mecanica teoretică (unghiurile lui Euler, unghiurile lui ***, etc.) [**], [**].

            Uneori se folosesc parametrizări neminimale ( de exemplu patru parametri reali legaţi între ei printr-o relaţie). Acesta este cazul parametrizărilor prin intermediul cuaternionilor unitari, parametrilor lui Euler, vectorul Rodrigues, etc. [**], [**].

 

2.6. Inelul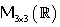

            Am demonstrat în paragraful 2.1 că mulţimea matricelor pătratice  are structură algebrică de grup abelian în raport cu operaţia de adunare. De asemenea,  are structură algebrică de monoid în raport cu operaţia de înmulţire.

 

            Folosind definiţiile operaţiilor de adunare şi înmulţire a matricelor din  se probează fără dificultate:

(D1)     ;

(D2)     .

 

            Cu proprietăţile (A1) – (A4), (M1) – (M2) şi (D1) – (D2) rezultă că mulţimea  are structură algebrică de inel cu unitate în raport cu operaţiile de adunare şi înmulţire.

            Acest inel este necomutativ (în general ) şi are divizori ai lui zero (există  astfel încât ).

 

2.7. 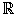-algebra

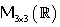
            Am demonstrat în paragraful 2.1. că  are structură de spaţiu liniar peste corpul numerelor reale , finit dimensional cu: .

            Notând , , , o bază în spaţiul liniar real  este  unde am notat cu „” produsul tensorial al matricelor coloană din  (III.A.45). Un element generic , se scrie:

(III.A.147)

 

            Operaţia de înmulţire a matricelor din  (III.A.108) are proprietăţile:

	(III.A.148)
	(III.A.149)
	(III.A.150)

 

            Cu operaţiile de adunare a matricelor, înmulţirea cu scalari reali şi înmulţirea acestora cu proprietăţile (III.A.148) – (III.A.150) se spune că -spaţiul liniar  este o -algebră asociativă.

            Deoarece:

astfel încât:

(III.A.151)

se spune că -algebră asociativă este cu unitate. Matricea  se numeşte unitatea algebrei.

            Proprietatea:

(III.A.152)

conferă -algebrei  proprietatea de -liniaritate.

 

            Vom spune că  este o algebră liniară, asociativă, cu unitate, peste corpul numerelor reale. -algebra  este necomutativă, cu divizori ai lui zero.

 

            Produsul a două elemente generice din :

	(III.A.153)
	(III.A.154)

se efectuează în conformitate cu proprietăţile (III.A.148) – (III.A.150) şi (III.A.152):

(III.A.155)

            Regula de înmulţire a elementelor bazei  se numeşte tabela de înmulţire a algebrei.

 

            Pentru determinarea tabelei de înmulţire a -algebrei  vom demonstra mai întâi:

 

            Teorema 14:

            Are loc identitatea:

(III.A.156)

 

            Demonstraţie:

            Fie :

	(III.A.157)
	(III.A.158)
	(III.A.159)
	(III.A.160)

            Avem:

	(III.A.161)
	(III.A.162)

            Folosind regula de înmulţire a matricelor pătratice se obţine:

(III.A.163)

unde:

(III.A.164)

            Am notat prin  produsul scalar al matricelor coloană , definit prin relaţia (III.A.25).

            ţinând seama de:

(III.A.165)

din (III.A.164) rezultă (III.A.156).    ♦

 

            Aplicând identitatea (III.A.156) se obţine:

(III.A.166)

            Cum baza  este ortonormată în :

(III.A.167)

din (III.A:166) urmează:

(III.A.168)

            Relaţia (III.A.168) reprezintă tabela de înmulţire în ‑algebra .

Observaţii:

            1º. Folosind tabela de înmulţire (III.A.168) relaţia (III.A.155) devine:

(III.A.169)

regăsindu-se astfel regula de înmulţire a două matrice pătratice.

 

            Vom defini acum aplicaţia notată „trace”:

(III.A.170)

numită şi urma matricei A. Urma unei matrice din  este suma elementelor diagonalei principale a matricei.

 

            Teorema 15:

            Au loc identităţile:

	(III.A.171)
	(III.A.172)
	(III.A.173)
	(III.A.174)
	(III.A.175)

 

            Demonstraţia teoremei este imediată folosind definiţia (III.A.170).

 

---