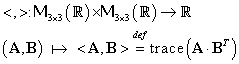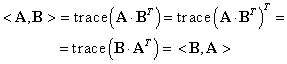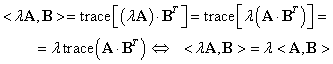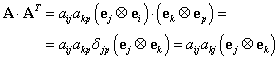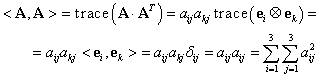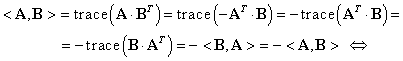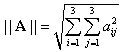2.8. Produsul scalar al matricelor din

            Vom defini aplicaţia notată „” prin:

(III.A.176)

 

           

 

Teorema 16:

            Aplicaţia definită prin (III.A.176) este un produs scalar pe .

 

            Demonstraţie:

            Vom demonstra că aplicaţia (III.A.176) are proprietăţile:

(SM1)  ;

(SM2)  ;

(SM3)  ;

(SM4)  ;   .

 

            Proprietatea (SM1) rezultă din:

(III.A.177)

 

            (SM2) rezultă din:

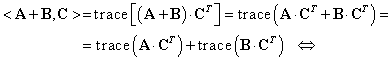
(III.A.178)

 

            Proprietatea (SM3) se obţine din:

(III.A.179)

 

            Pentru a demonstra proprietatea (SM4) considerăm un element oarecare , pentru care:

(III.A.180)

de unde avem şi:

(III.A.181)

            Din (III.A.180) şi (III.A.181), ţinând cont de (III.A.166), rezultă:

(III.A.182)

            Din (III.A.182), cu (III.A.173), avem:

(III.A.183)

            Prin urmare:

(III.A.184)

            Cum , din (III.A.183) se obţine:

(III.A.185)

şi:

(III.A.186)

            Teorema este astfel demonstrată.     ♦

 

            Această teoremă arată că -spaţiul liniar  este un spaţiu prehilbertian.

 

Observaţii:

            1º. Baza  din -spaţiul liniar  este ortonormată. Folosind definiţia produsului scalar (III.A.176) şi faptul că baza  este ortonormată în  se obţine:

(III.A.187)

adică:

(III.A.188)

 

            2º. Orice matrice antisimetrică din  este ortogonală pe orice matrice simetrică din . Într-adevăr, fie :

(III.A.189)

şi :

(III.A.190)

            Avem succesiv:

	(III.A.191)

            Vom scrie simbolic acest lucru în forma:

(III.A.192)

            Descompunerea spaţiului liniar  în suma directă dată de teorema 8 este aşadar şi o descompunere în subspaţii liniare ortogonale în raport cu produsul scalar dat de relaţia (III.A.176).

 

            3º. Produsul scalar (III.A.176) permite definirea aplicaţiei:

(III.A.193)

            Dacă , atunci avem:

(III.A.194)

            Aplicaţia (III.A:193) este o normă pe , indusă de produsul scalar (III.A.176). Au loc proprietăţile:

(NM1)             ;   ;

(NM2)             ;

(NM3)             ;

care se demonstrează folosind proprietăţile ale produsului scalar.

            În plus, are loc şi:

(NM4)             .

            Cu norma dată de relaţia (III.A.193) şi proprietatea (NM4) -algebra  se numeşte -algebră normată [**], [**].

            Faptul că  este -algebră normată permite definirea convergenţei şirurilor şi seriilor de matrice din  şi apoi definirea limitei şi continuităţii funcţiilor matriceale.

---