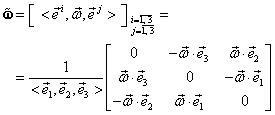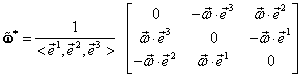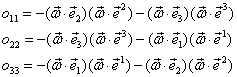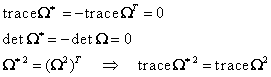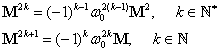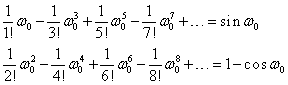III.7. Soluţie:

            a. Relaţiile (III.7.1) – (III.7.4) reprezintă tocmai ecuaţiile caracteristice ale celor patru matrice. Aceste ecuaţii se determină utilizând relaţiile (III.4.11) - (III.4.14).

            Matricea  este dată de (III.2.1):

(III.7.6)

            Calculăm apoi:

   cu:

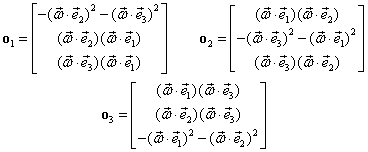
(III.7.7)

            ţinând cont de (III.7.6) şi (III.7.7) rezultă că invarianţii principali ai matricei  sunt:

	(III.7.8)

 

            Ecuaţia caracteristică (III.4.14) a matricei  este:

(III.7.9)

            Aplicând teorema Cayley-Hamilton se obţine:

(III.7.10)

            Relaţia (III.7.1) este astfel demonstrată.

 

            Procedând în acelaşi mod pentru matricea  obţinem:

(III.7.11)

şi:

   cu:

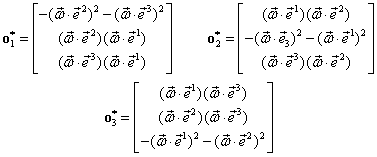
(III.7.12)

            Invarianţii principali ai matricei  sunt daţi de:

	(III.7.13)

iar ecuaţia sa caracteristică este:

(III.7.14)

            Aplicând teorema Cayley-Hamilton se obţine:

(III.7.15)

            Relaţia (III.7.2) este deci satisfăcută.

 

            Pentru matricea  (III.2.7) avem:

(III.7.16)

            Elementele de pe diagonala principală a matricei ,  sunt:

(III.7.17)

astfel încât se obţine:

	(III.7.18)

 

            Ecuaţia caracteristică a matricei  este:

(III.7.19)

            Prin aplicarea teoremei Cayley-Hamilton rezultă:

(III.7.20)

            Relaţia (III.7.3) este demonstrată.

 

            ţinând cont de (III.2.53) se obţine:

(III.7.21)

de unde rezultă:

(III.7.22)

            Invarianţii principali ai matricei  sunt:

(III.7.23)

            Matricele  şi  au aceeeaşi invarianţi principali, deci au aceeaşi ecuaţie caracteristică (III.7.19). Prin aplicarea teoremei Cayley-Hamilton rezultă:

(III.7.24)

            Relaţia (III.7.4) este demonstrată.

 

            b. Se observă că ecuaţiile matriceale satisfăcute de cele patru matrice studiate au aceeaşi formă:

(III.7.25)

unde constanta  este:

(III.7.26)

 

            Ipoteza  este echivalentă cu .

            Pentru matricea M care satisface ecuaţia (III.7.25) considerăm seria:

(III.7.27)

            Din relaţia (III.7.25) rezultă:

(III.7.28)

            Prin inducţie matematică după  se demonstrează că:

(III.7.29)

            Cu expresiile (III.7.29) seria (III.7.27) devine:

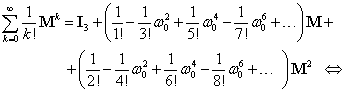
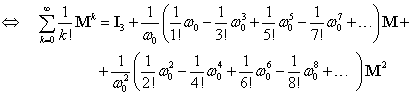
(III.7.30)

            Se ştie că seriile numerice următoare sunt convergente şi:

(III.7.31)

 

            Din relaţiile (III.7.5), (III.7.30) şi (III.7.31) rezultă că exponenţiala unei matrice care satisface ecuaţia (III.7.25) are forma:

(III.7.32)

 

            Pentru matricea M care satisface ecuaţia (III.7.25) avem: . Determinantul matricei exponenţiale  este dat de:

(III.7.33)

Rezultă că matricea  este inversabilă. Inversa acestei matrice este:

(III.7.34)

            ţinând cont de relaţiile (III.7.32) şi (III.7.34) rezultă:

(III.7.35)

---