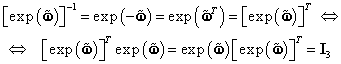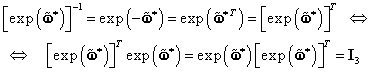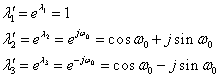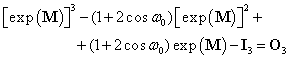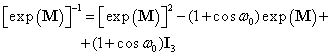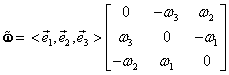Aplicăm relaţiile (III.7.32) şi (III.7.35) pentru a determina exponenţialele celor patru matrice studiate si inversele acestora. ţinând cont de (III.7.26) se obţine:
|
|
(III.7.36) |
|
|
(III.7.37) |
|
|
(III.7.38) |
|
|
(III.7.39) |
cu 
dat de (III.7.26).
Inversele acestor matrice sunt:
|
|
(III.7.40) |
|
|
(III.7.41) |
|
|
(III.7.42) |
|
|
(III.7.43) |
Observaţii:
1. Deoarece
matricele 
şi
sunt
antisimetrice (
, 
)
rezultă că matricele 
şi 
sunt matrice ortogonale:
|
|
(III.7.44) |
|
|
(III.7.45) |
2. Matricele
şi 
sunt legate prin
relaţia (III.2.53):
|
|
(III.7.46) |
Din această relaţie rezultă:
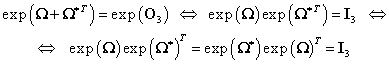
(III.7.47)
3. Dacă matricea M satisface ecuaţia (III.7.25):
|
|
(III.7.48) |
, 
exponenţiala matricei M este dată de (III.7.32):
|
|
(III.7.49) |
Valorile proprii ale matricei M, rădăcinile ecuaţiei:
|
|
(III.7.50) |
sunt 
, 
, 
.
Valorile proprii ale matricei 
(III.7.49) sunt:
|
|
(III.7.51) |
Ecuaţia caracteristică a matricei 
, care admite
rădăcinile 
şi
, este:
|
|
(III.7.52) |
Aplicând teorema Cayley-Hamilton pentru
matricea se
obţine:
|
|
(III.7.53) |
Înmulţind ecuaţia (III.7.53)
cu matricea 
se
obţine pentru matricea expresia:
|
|
(III.7.54) |
Înlocuind în relaţia (III.7.54) matricea cu expresia sa dată de (III.7.49) rezultă:
|
|
(III.7.55) |
Se observă că expresia (III.7.55) coincide cu expresia (III.7.35) determinată anterior.
4.
În spaţiul liniar al vectorilor liberi 
efectuăm o schimbare de baze de la
baza 
(cu baza reciprocă 
)
la baza 
(cu baza reciprocă 
)
(vezi problema I.26) cu matricea schimbării de baze:
|
|
(III.7.56) |
, 
Aşa cum s-a demonstrat în
observaţia 3 de la problema III.2 matricele
şi 
asociate unui
vector 
în
baza 
sunt
asemenea cu matricele , respectiv , asociate aceluiaşi vector în
baza 
deoarece:
|
|
(III.7.57) |
|
|
(III.7.58) |
Dacă două matrice pătratice cu elemente numere
reale atunci au aceeaşi ecuaţie caracteristică. Se observă că: coeficienţii
ecuaţiei caracteristice a matricei nu depind de baza aleasă în spaţiul
liniar 
.
ţinând cont de relaţiile (III.7.57), (III.7.58) rezultă că între exponenţiale acestor matrice există relaţiile:
|
|
(III.7.59) |
|
|
(III.7.60) |
Matricele şi 
(respectiv
şi 
) sunt asemenea numai în cazul în care
matricea 
a
schimbării de baze este ortogonală (
), caz în
care există relaţiile (III.2.79), (III.2.80):
|
|
(III.7.61) |
|
|
(III.7.62) |
În acest caz matricele şi (respectiv şi ) au
aceeaşi ecuaţie caracteristică. De asemenea se obţine:
|
|
(III.7.63) |
|
|
(III.7.64) |
5.
Dacă baza este
ortonormată, pentru un vector 
, 
, matricele , , şi coincid fiind egale cu:
|
|
(III.7.65) |
În acest caz ecuaţia caracteristică a matricei este:
|
|
(III.7.66) |
de unde rezultă:
|
|
(III.7.67) |
Relaţiile (III.7.32) şi (III.7.40) implică:
|
|
(III.7.68) |
|
|
(III.7.69) |
 |
  |