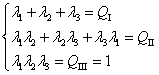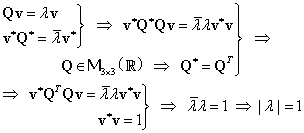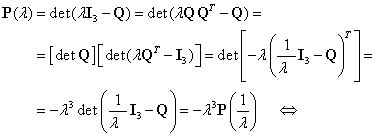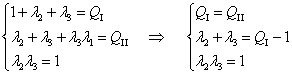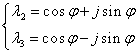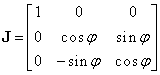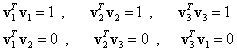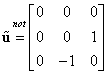III.8. Soluţie:

            Fie  polinomul caracteristic al matricei Q. Conform relaţiilor (III.4.10)-(III.4.13) acest polinom are forma:

(III.8.1)

unde coeficienţii  reprezintă invarianţii principali ai matricei Q şi au expresiile:

	(III.8.2)
	(III.8.3)
	(III.8.4)

            Valorile proprii ale matricei Q, rădăcinile ecuaţiei , notate , satisfac relaţiile lui Viéte:

(III.8.5)

 

 

 

 

 

            Din condiţia de ortogonalitate a matricei Q rezultă că valorile proprii ale matricei Q, rădăcinile ecuaţiei , notate , sunt plasate pe cercul unitate cu centrul în originea planului complex, adică .

            Considerând  vectorul propriu corespunzător valorii proprii . Vectorul propriu v poate fi ales unitar, adică astfel încât să fie satisfăcută relaţia: , unde  reprezintă matricea obţinută prin transpunerea matricei v şi conjugarea elementelor sale. În acest caz se obţine:

(III.8.5)

 

            Deoarece matricea ortogonală Q este proprie () se obţine:

	(III.8.6)

            În particular, pentru , din (III.8.6) se obţine , deci  este valoare proprie a matricei Q. Din relaţiile lui Viéte (III.8.5) rezultă:

(III.8.7)

 

            Deoarece polinomul  are coeficienţi reali, sunt posibile următoarele situaţii:

a. , caz în care din ecuaţia (III.8.7)₃ rezultă:

astfel încât

(III.8.8)

b. .

 

            a. Dacă relaţiile (III.8.8) sunt satisfăcute, din relaţiile (III.8.7) se obţine:

(III.8.9)

            ţinând cont de relaţia (III.8.2), se obţine:

astfel încât

(III.8.10)

            În plus, se observă că în acest caz urma matricei Q satisface:

(III.8.11)

            Deci, dacă pentru o matrice ortogonală proprie relaţia (III.8.11) este satisfăcută, atunci există unghiul  unic determinat de relaţia:

(III.8.12)

 

            Matricea Jordan asociată matricei ortogonale Q are forma:

(III.8.13)

            Notăm cu , matricea pătratică formată cu vectorii proprii  ai matricei Q. Matricea T satisface relaţia:

(III.8.14)

deci matricea Q este asemenea cu matricea J.

            Vectorii proprii ai matricei Q pot fi aleşi de normă egală cu 1. În plus, deoarece valorile proprii ale matricei Q sunt distincte, vectorii proprii sunt ortogonali. Scriind matricea T sub forma , aceste condiţii se conduc la:

(III.8.15)

            Relaţiile (III.8.15) arată că matricea T este ortogonală:

(III.8.16)

            Se observă că matricea Jordan (III.8.13) poate fi scrisă sub forma:

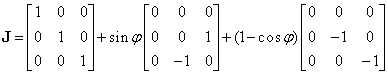
(III.8.17)

            Notăm cu  matricea antisimetrică:

(III.8.18)

            Se observă că această matrice satisface:

	(III.8.19)
	(III.8.20)

            Cu notaţia (III.8.18), matricea Jordan (III.8.17) devine:

(III.8.21)

            În acelaşi mod ca şi în problema III.7 se poate determina exponenţiala:

(III.8.22)

            Comparând relaţiile (III.8.21) şi (III.8.22) se poate trage concluzia:

(III.8.23)

            Deoarece matricele Q şi J sunt asemenea (III.8.14), rezultă în continuare:

(III.8.24)

            Notăm:

(III.8.25)

            Deoarece matricea T este ortogonală (III.8.22) şi matricea  este antisimetrică rezultă că matricea  este antisimetrică:

(III.8.26)

            De asemenea. matricea definită prin:

(III.8.27)

cu  dat de relaţia (III.8.12) este antisimetrică.

            Cu această notaţie, din (III.8.24) rezultă:

(III.8.28)

 

Observaţii:

            1º. Din relaţiile (III.8.22)-(III.8.25) se obţine că matricea  poate fi scrisă sub forma:

(III.8.29)

            ţinând cont că matricea  este antisimetrică şi  este simetrică, din (III.8.29) rezultă că matricea  poate fi determinată direct:

(III.8.30)

 

 Din relaţiile (III.8.20) şi (III.8.25) ecuaţia caracteristică a matricei   este obţinută sub forma:

(III.8.31)

            Considerăm matricea  ca fiind matricea antisimetrică asociată unui vector , , prin izomorfismul  (III.2.1) în ipoteza că baza  fixată în  este ortonormată orientată drept:

(III.8.32)

            Comparând ecuaţia (III.8.31) cu (III.7.67) rezultă că vectorul  este unitar, .

 

            Deci pentru o matrice ortogonală proprie Q pentru care  există un unghi  şi o matrice coloană , cu proprietatea , unic determinaţi prin:

	(III.8.33)
	(III.8.34)

astfel încât:

(III.8.35)

 

            Se poate demonstra că matricea coloană  (asociată vectorului ) este vector propriu al matricei  corespunzător valorii proprii :

(III.8.36)

deoarece:

(III.8.37)

---