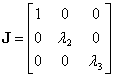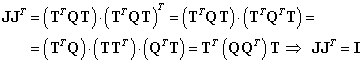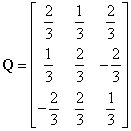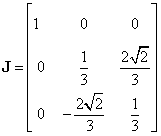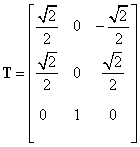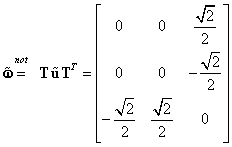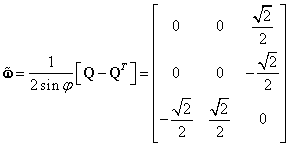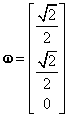b.1. Dacă toate valorile proprii ale matricei Q sunt numere reale distincte, atunci matricea Jordan asociată matricei ortogonale Q are forma:

(III.8.29)

            Notăm cu , matricea pătratică formată cu vectorii proprii  ai matricei Q. Deoarece valorile proprii ale matricei Q sunt distincte, vectorii proprii pot fi aleşi astfel încât să fie unitari şi ortogonali, deci astfel încât matricea T să fie ortogonală:

(III.8.30)

            Din relaţiile (III.8.14) şi (III.8.30) rezultă că şi matricea Jordan asociată matricei Q este ortogonală, deoarece:

(III.8.31)

            ţinând cont de forma (III.8.29) a matricei Jordan, relaţia (III.8.13) implică:

(III.8.32)

care împreună cu relaţia (III.8.7)₃ duc în final la , ceea ce contrazice ipoteza . Deci această situaţie nu este posibilă.

 

            b.2. În cazul în care matricea ortogonală proprie are toate valorile proprii egale cu 1, polinomul caracteristic al matricei Q devine . Polinomul minimal al matricei Q este . Deoarece orice matrice pătratică satisface ecuaţia matriceală corespunzătoare polinomului său minimal, , se obţine . Matricea unitate este matrice ortogonală proprie şi poate fi scrisă ca exponenţiala matricei nule, , unde este matrice antisimetrică.

 

Observaţii:

            1º. Şi în acest caz matricea  poate fi pusă sub forma (III.8.35), deoarece .

 

            b.3. Dacă valorile proprii ale matricei  sunt:  

 

 

            În concluzie, orice matrice ortogonală proprie poate fi scrisă ca exponenţiala unei matrice antisimetrice.

 

 

Observaţii:

            2º. Interpretarea geometrică a acestor relaţii **** este următoarea: dacă în spaţiul liniar al vectorilor liberi  se alege o bază ortonormată dreaptă, matricea  reprezintă matricea rotaţiei în jurul vectorului  de unghi egal cu , măsurat în planul perpendicular pe . Sensul de măsurare a acestui unghi şi sensul vectorului  sunt asociate prin regula burghiului drept (figura III. *). Matricea coloană v asociată vectorului  obţinut prin rotirea vectorului  în jurul vectorului  de unghi  este de forma:

(III.8.40)

unde  este matricea coloană asociată vectorului . Vectorii coliniari cu  rămân nemodificaţi.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

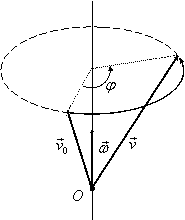Figura III.

 

            Pentru  matrice antisimetrică de ordinul 3, matricea  reprezintă matricea rotaţiei în jurul vectorului  cu viteza unghiulară .

 

 

 

 

 

 

 

 

 

 

 

 

 

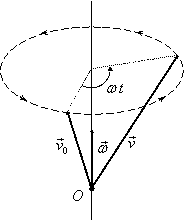Figura III.

 

            Acest mod de interpretarea este utilizat în studiul mişcării de rotaţie a unui corp rigid în jurul unui punct fix unde intervine aşa-numita matrice de rotaţie care este o matrice ortogonală proprie.

 

Exemplu numeric:

Soluţia I:

            Considerăm matricea ortogonală proprie:

(III.8.41)

            Se observă că . Notăm cu  unghiul definit prin:

(III.8.42)

            Polinomul caracteristic al matricei Q este:

(III.8.43)

iar valorile proprii ale acestei matrice sunt:

(III.8.44)

            ţinând cont de (III.8.19), matricea Jordan asociată matricei Q este:

(III.8.45)

            Vectorii proprii unitari ai matricei Q, coloanele matricei , se determină din condiţia:

(III.8.46)

            Se obţine:

(III.8.47)

            Se observă că matricea T este ortogonală, . Matricea Jordan (III.8.39) este exponenţiala matricei  cu  dat de relaţia (III.8.36) şi  dat de (III.8.24).

Se pot determina deci matricele antisimetrice:

	(III.8.48)
	(III.8.49)

astfel încât matricea Q satisface relaţia:

(III.8.50)

 

Soluţia II:

            Cu unghiul  dat de relaţia (III.8.42) determinăm matricea  cu ajutorul relaţiei (III.8.33):

(III.8.51)

de unde rezultă şi vectorul propriu unitar corespunzător valorii proprii  sub forma:

(III.8.52)

care coincide cu prima coloană a matricei T (III.8.47).

            Se observă că se ajunge la acelaşi rezultat ca şi în prima soluţie, dar mult mai rapid.

---

GO TOP